判断题。（对的在括号里画“√”，错的在括号里画“×”）1．第29届奥运会2008年在北京举行，这一年的上半年一共有182天。[]2．把米长的绳子平均分成4段，每段占全长的。[]3．把25克糖溶-六年级数学打印页面

判断题。（对的在括号里画“√”，错的在括号里画“×”）1．第29届奥运会2008年在北京举行，这一年的上半年一共有182天。[]2．把米长的绳子平均分成4段，每段占全长的。[]3．把25克糖溶-六年级数学

[db:作者] 2019-06-04 08:00:00 零零社区

题文

判断题。（对的在括号里画“√”，错的在括号里画“×”）

1．第29届奥运会2008年在北京举行，这一年的上半年一共有182天。

[     ]

2．把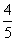米长的绳子平均分成4段，每段占全长的。

[     ]

3．把25克糖溶解于100克水中，那么这种糖水的含糖率为25%。

[     ]

4．给一间教室铺地砖，每块地砖的面积和所需地砖的块数成反比例。

[     ]

5．甲数的等于乙数的，那么甲数和乙数的比是6：5。

[     ]
题型：判断题  难度：中档

答案

1.√；2.×；3.×；4.√；5.×

据专家权威分析，试题“判断题。（对的在括号里画“√”，错的在括号里画“×”）1．第29届奥运会..”主要考查你对比的应用，分数的认识及意义，年，月，日，百分数的计算，百分数的应用题，正比例的意义，反比例的意义等考点的理解。关于这些考点的“档案”如下：

比的应用分数的认识及意义年，月，日百分数的计算，百分数的应用题正比例的意义，反比例的意义

考点名称：比的应用

比的应用:
根据各部分的比，确定各部分与总量之间的关系，即各部分占总量的几分之几，然后按照“求一个数（这里指分配的量）的几分之几是多少”的问题解答。
一般单位要统一，注意比的前后要一致，就是等号两边都是图上距离与实际距离的比，或者是反过来，再就是注意大的比大的，等于小的比小的。

考点名称：分数的认识及意义

分数的认识：
1、单位“1”

2、分数
把单位“1”平均分成若干份，表示这样一份或者几份的数叫做分数。
如：

一堆糖，平均分成2份，每份是这堆糖的
一堆糖，平均分成3份，2份是这堆糖的
一堆糖，平均分成4份，3份是这堆糖的
一堆糖，平均分成6份，5份是这堆糖的

3、分数单位：表示其中一份的数就是分数单位。如的分数单位是
分数的意义：
把一个物体或一个计量单位平均分成若干份，这样的一份或几份可用分数表示。在分数里，中间的横线叫做分数线；分数线下面的数叫做分母，表示把单位“1”平均分成多少份；分数线上面的数叫做分子，表示有这样的多少份。

考点名称：年，月，日

时间单位：
日（天）、星期、月、年、世纪。

月：
大月（31天）：一月、三月、五月、七月、八月、十月、十二月；
小月：四月、六月、九月、十一月；
二月：平年28天，闰年29天。

季度：
一年有四个季度：1月、2月、3月属于第一季度；4月、5月、6月属于第二季度；7月、8月、9月属于第三季度；10月、11月、12月属于第四季度。

年：
闰年：通常公历年是4的倍数的是闰年；公历年份是整百数的，须是400的倍数，闰年有366天。
平年：通常公历年不是4的倍数的是平年；公历年份是整百数的，不是400的倍数的是平年，平年有365天。
时间单位之间的进率：
世纪年月；1日（天）=24小时；1星期=7天。

闰年的判断方法：
公历年份可被4整除为闰年，但是正百的年数必须是可以被400整除的才是闰年。

考点名称：百分数的计算，百分数的应用题

常见的百分数的计算方法：
百分数应用题关系式：
利息的计算公式：利息=本金×利率×时间。
百分率：例：发芽率=发芽种子数÷试验种子数×100%
利率=利息÷本金×100%
折数=现价÷原价
成数=实际收成÷计划收成
税率=应纳税额÷总收入×100%
利润=售出价-成本，利润率=利润÷成本×100%=（售出价÷成本-1）×100%
折扣=实际售价÷原售价×100%（折扣<1）
浓度问题：
溶质的重量+溶剂的重量=溶液的重量；
溶质的重量÷溶液的重量×100%=浓度；
溶液的重量×浓度=溶质的重量；
溶质的重量÷浓度=溶液的重量。

考点名称：正比例的意义，反比例的意义

正比例：
两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量相对应的两个数的比值（也就是商）一定，这两种量就叫做成正比例的量，它们的关系叫做正比例关系，正比例的图像是一条直线；
用字母表示为如果用字母x和y表示两种相关联的量，用k表示它们的比值（一定），正比例关系可以用以下关系式表示：=k（一定）；
正比例关系两种相关联的量的变化规律：同时扩大，同时缩小，比值不变．正比例和反比例

反比例：
两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量相对应的两个数的积一定，这两种量就叫做成反比例的量，它们的关系叫做反比例关系；
如果用字母x和y表示两种相关联的量，用k表示它们的积，反比例关系可以用下面关系式表示：xy=k（一定）。
反比例的意义：
成反比例的量包括三个数量，一个定量和两个变量。研究两个变量之间的扩大（或缩小）的变化关系。一种量发生变化，引起另一种量发生相反的变化。这两种量是反比例的量，它们的关系成反比例关系。
成反比例的量：
前提：两种相关的量（乘法关系）
要求：一个量变化，另一个量也随着变化，并且，这两个量中相对应的两个数的乘积一定。
结论：这两个量就叫做反比例的量，它们的关系叫做反比例关系。
正比例和反比例关系：
相同点：
①正比例和反比例都含有三个数量，在这三个数量中，均有一个定量、两个变量。
②在正、反比例的两个变量中，均是一个量变化，另一个量也随之变化。并且变化方式均属于扩大（乘以一个数）或缩小（除以一个数）若干倍的变化。
不同点：
①正比例的定量是两个变量中相对应的两个数的比值。反比例的定量是两个变量中相对应的两个数的积。
②正比例的图像时上升直线；反比例是曲线。
③公式不同：正比例是（=k（一定）），反比例是（xy=k（一定））。
④规律不同：正比例是一个数缩小，另一个数也缩小，一个数扩大，另一个数也扩大；反比例是一个数缩小，另一个数就扩大，一个数扩大另一个数就缩小。　
判断两种量成正比例、反比例或不成比例的方法：
（1）找出两种相关联的量。
（2）根据两种相关联的量之间的关系列出数量关系式。
（3）如果两种量中相对应的两个数的比值（也就是商）一定，就是成正比例的量；若积一定，就是反比例的量。

http://www.00-edu.com/ks/shuxue/1/bideyingyong/2019-06-04/1176614.html十二生肖
十二星座