零零教育信息网 首页 > 考试 > 物理 > 初中物理 > 液体压强的计算 > 正文 返回　打印

如图所示，在横截面积为5×10-2m2的圆柱形容器中盛有一定质量的水，已知在距离容器底部0.1m处水的压强为4.0×103Pa，现把一体积为5×10-3m3的木块投入水中，测得水面上升了0.-物理
[db:作者]  2020-04-23 00:00:00  零零社区

题文

如图所示，在横截面积为5×10-2m2的圆柱形容器中盛有一定质量的水，已知在距离容器底部0.1m处水的压强为4.0×103Pa，现把一体积为5×10-3m3的木块投入水中，测得水面上升了0.08m．（g取10N/kg）
求：（1）木块的质量；
（2）木块放入水中后，容器底受到的压强；
（3）容器内水的质量．

题型：问答题  难度：中档

答案

（1）木块排开水的体积：
V排=S△h=5×10-2m2×0.08m=4×10-3m2，
根据阿基米德原理可得，木块受到的浮力：
F浮=ρgV排=1.0×103kg/m3×10N/kg×4×10-3m2=40N，
∵木块漂浮，
∴G木=F浮=40N，
∵G=mg，
∴木块的质量m木=
G木
g
=
40N
10N/kg
=4kg；
（2）设容器内水的深度为h，则距离容器底部0.1m处水的压强：
p=ρg（h-0.1m）=1.0×103kg/m3×10N/kg×（h-0.1m）=4.0×103Pa，
解得：h=0.5m，
木块放入水中后，水的深度：
h′=0.5m+0.08m=0.58m，
容器底受到的压强：
p′=1.0×103kg/m3×10N/kg×0.58m=5.8×103Pa；
（3）容器内水的体积：
V水=Sh=5×10-2m2×0.5m=2.5×10-2m3，
容器内水的质量：
m水=ρV水=1.0×103kg/m3×2.5×10-2m3=25kg．
答：（1）木块的质量为4kg；
（2）木块放入水中后，容器底受到的压强为5.8×103Pa；
（3）容器内水的质量为25kg．

据专家权威分析，试题“如图所示，在横截面积为5×10-2m2的圆柱形容器中盛有一定质量的水..”主要考查你对  液体压强的计算，压强的大小及其计算，密度公式的应用，重力的计算  等考点的理解。关于这些考点的“档案”如下：

液体压强的计算压强的大小及其计算密度公式的应用重力的计算

考点名称：液体压强的计算

  • 液体压强的计算公式：
    P=ρgh（ρ是液体密度，单位是千克/米3；g=9.8牛/千克；h是深度，指液体自由液面到液体内部某点的竖直距离，单位是米。）

  • 对液体压强公式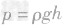的理解
    1．由公式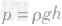可知，液体内部的压强只跟液体的密度和深度有关，而跟液体的质量、重力、体积以及容器的形状、底面积等无关。

    2．公式只适用于计算静止的液体产生的压强，而对固体、气体或流动的液体均不适用。

    3．在液体压强公式中h表示深度，而不是高度。判断出h的大小是计算液体压强的关键，如图所示，甲图中A点的深度为30cm，乙图中B点的深度为 40cm．丙图中C点的深度为50cm。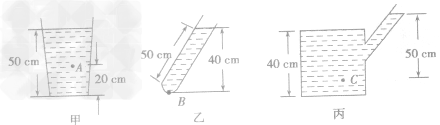

    4．运用公式时应统一单位：ρ的单位用kg／m3，h 的单位用m，计算出的压强单位才是Pa。 

    5．两公式的区别与联系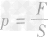：是压强的定义式，  无论固体、液体还是气体，它都是普遍适用的；而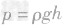是结合液体的具体情况通过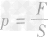推导出来的，所以适用于液体。

    6．用公式求出的压强是液体由于自身重力产生的压强，它不包括液体受到的外加压强。

    转换法和控制变量法探究液体压强大小跟哪些因素有关：
         在探究液体压强的大小时，由于液体压强的大小不易测量或是不能直接观测到它的大小，我们用“转换法”，通过液体压强计中两玻璃管液面的高度差的大小来比较液体压强的大小，将抽象的东西变成了直观且形象的东两，使问题简化了。

        由于液体内部压强跟液体的深度和液体密度两方面因素有关，所以在探究液体内部压强的规律时要采用控制变量法，即在探究液体压强与深度的关系时，要保持液体密度不变，在探究液体压强与液体的密度关系时，要保持液体的深度不变。

考点名称：压强的大小及其计算

  • 计算公式：
    P=F/S，式中p单位是：帕斯卡，简称：帕，1帕=1牛/米2，压力F单位是：牛；受力面积S单位是：米2。

  • 对压强公式的理解：
    1．此公式适用于任何情况，即固体、液体、气体的压强计算都可用此公式。

    2．此公式中各物理量单位分别是p→Pa、F→N、s→m2。在计算物体的压强时，只有当F的单位为N，S 的单位为m2时，压强的单位才能是Pa，因此在计算中必须统一单位。

    3．一张报纸平放时对桌子的压强约0．5Pa。成人站立时对地面的压强约为1．5×104Pa，它表示：人站立时，其脚下每平方米面积上，受到脚的压力为1．5× 104N。

    4．公式中的，是压力而不是重力。即使在某些情况下，压力在数值上等于物体所受的重力，也不应把公式直接写成，而应先注明F=G得：。

    5．公式中的受力面积S，是指受力物体发生形变的那部分面积，也就是两物体的实际接触面积，而不一定是受力物体的表面积。如图所示，一个圆台形物体置于水平地面上，分别采用A、B两种方式放置，对地面的压力不变，但图A中受力面积是S2，图B中受力面积为S1，而它们都与水平地面的面积大小无关。

    6.  由公式推导出F=pS和可用于计算压力和受力面积的大小。

    巧用求柱体压强：
      将一密度均匀、高为h的圆柱体放在水平桌面上，桌面受到的压强，所圆柱体(包括长方体、正方体等)产生的压强，只与固体的密度和高度有关，而与固体的重力、体积和底面积因素无关，应用公式就给解这类题带来很大方便。
    例1如图所示，两圆柱形铁柱的底面半径之比是 3：1，高度相同，则它们对水平地面的压强之比为（   ）

    A．3：1B．1：3C．1：1D．9：l
    解析：本题是分析圆柱体的压强，可直接利用公式进行分析。因为两圆柱体的密度相同、高度相同，所以压强相同，选项C正确。
    答案：C

考点名称：密度公式的应用

  • 密度公式的应用：
    （1）利用m=ρV求质量；利用V=m/ρ求体积

    （2）对于密度公式，还要从以下四个方面理解
    ①同种物质，在一定状态下密度是定值，它不随质量大小或体积大小的改变而改变。当其质量（或体积）增大几倍时，其体积（或质量）也随着增大几倍，而比值是不变的。因此，不能认为物质的密度与质量成正比，与体积成反比；
    ②具有同种物质的物体，在同一状态下，体积大的质量也大，物体的体积跟它的质量成正比；
    ③具有不同物质的物体，在体积相同的情况下，密度大的质量也大，物体的质量跟它的密度成正比；

    ④具有不同物质的物体，在质量相同的条件下，密度大的体积反而小，物体的体积跟它的密度成反比。

  • 密度公式的应用：
    1. 有关密度的图像问题
    此问题一般是给出质量一体积图像，判断或比较物质密度。解答时可在横坐标(或纵坐标)任选一数值，然后在纵坐标(或横坐标)上找到对应的数值，进行分析比较。
     例1如图所示，是甲、乙两种物质的m一V图像，由图像可知(   )
    A．ρ甲>ρ乙
    B．ρ甲=ρ乙
    C．ρ甲<ρ乙
    D．无法确定甲、乙密度的大小

    解析:要从图像直接看出甲、乙两种物质的密度大小目前还做不到，我们要先借助图像，根据公式ρ =总结规律后方可。
    如图所示，在横轴上任取一点V0，由V0作横轴的垂线V0B，分别交甲、乙两图线于A、B两点，再分别从A、B两点作纵轴垂线，分别交纵轴于m甲、m乙两点。则甲、乙两种物质的密度分别为，ρ乙= ，因为m甲<m乙，所以ρ甲<ρ乙，故C正确。

    2. 密度公式ρ =及变形、m=ρV的应用：
    密度的公式是ρ =，可得出质量计算式m=ρV 和体积计算式。只要知道其中两个物理量，就可以代入相应的计算式进行计算。审题时注意什么量是不变的，什么量是变化的。
    例2某瓶氧气的密度是5kg/m3，给人供氧用去了氧气质量的一半，则瓶内剩余氧气的密度是_____；容积是10L的瓶子装满了煤油，已知煤油的密度是 0．8×103kg/m3，则瓶内煤油的质量是_____，将煤油倒去4kg后，瓶内剩余煤油的密度是______。
     解析：氧气用去一半，剩余部分仍然充满整个氧气瓶，即质量减半体积不变，所以氧气的密度变为 2．5kg/m3。煤油倒去一半后，体积质量同时减半，密度不变。
    答案：2．5kg/m3；8kg；0．8×10kg/m3。

    3. 比例法求解物质的密度
       利用数学的比例式来解决物理问题的方法称之为 “比例法”。能用比例法解答的物理问题具备的条件是：题目所描述的物理现象，由初始状态到终结状态的过程中至少有一个量保持不变，这个不变的量是由初始状态变成终结状态的桥梁，我们称之为“中介量”。
    例3甲、乙丽个物体的质量之比为3：2，体积之比为l：3，那么它们的密度之比为(   )
    A．1：2B．2：1C．2：9D．9：2
    解析：（1）写出所求物理量的表达式：，
    （2）写出该物理量比的表达式：

    （3）化简：代入已知比值的求解：


    密度、质量、体积计算中的“隐含条件” 问题：
      很多物理问题中的有些条件需要仔细审题才能确定，这类条件称为隐含条件。因此寻找隐含条件是解决这类问题的关键。以密度知识为例，密度计算题形式多样，变化灵活，但其中有一些题具有这样的特点：即质量、体积、密度中的某个量在其他量发生变化时保持不变，抓住这一特点，就掌握了求解这类题的规律。

    1．隐含体积不变
    例1一个瓶子最多能装0．5kg的水，它最多能装_____kg的水银，最多能装_____m3的酒精。 ρ水银=13．6×103kg／m3，ρ水=1．0×103kg／m3，ρ酒精= 0．8×103kg／m3)
    解析:最多能装即装满瓶子，由最多装水量可求得瓶子的容积为V=5×10-4m3，则装水银为m水银=13．6×103kg／m3×5×10-4m3=6．8kg。装酒精的体积为瓶子的容积。
    答案6．8；5×10-4

    2. 隐含密度不变
    例2一块石碑的体积为V样=30m3，为测石碑的质量，先取了一块刻制石碑时剔下来的小石块作为样品，其质量是m样=140g，将它放入V1=100cm3的水中后水面升高，总体积增大到V2=150cm3，求这块石碑的质量m碑。
    解析：此题中隐含的条件是石碑和样品是同种物质，密度相同，而不同的是它们的体积和质量。依题意可知，样品体积为：
    V样=V2-V1=150cm3一100cm3=50cm3 =5．0×10-5m3
    得=84t
    答案：84t

    3. 隐含质量不变
    例3质量为450g的水结成冰后，其体积变化了 ____m3。(ρ水=0．9×103kg／m3)
    解析：水结成冰后，密度减小，450g水的体积为，水结成冰后，质量不变，因此冰的体积为=500cm3=5．0×10-4m3，=5．0× 10-4m3一4．5×10-4m3=5×10-5m3。

    合金物体密度的相关计算：
         首先要抓住合金体的总质量与总体积分别等于各种物质的质量之和与体积之和这一特征，然后根据具体问题，灵活求解。
    例两种不同的金属，密度分别为ρ1、ρ2：
    (1)若墩质量相等的金属混合后制成合金，则合金的密度为____。
    (2)若取体积相等的金属混合后制成合金，则合金的密度为_____。
    解析：这道题的关键是抓住“两总”不变，即总质量和总体积不变。在(1)中，两种金属的质量相等，设为m1=m2=m，合金的质量m总=2m，则密度为ρ1的金属的体积V1=，密度为ρ2的金属的体积V2=，合金的体积，则合金的密度
    在（2）中两种金属的体积相等，设为，合金的体积，密度为ρ1的金属的质量m1=，密度为ρ2的金属的质量为，合金的质量m总，合金的密度为。
    答案：
    注意：上述规律也适用于两种液体的混合，只要混合液的总质量和总体积不变即可。

考点名称：重力的计算

  • 重力的计算公式：
    物体所受的重力跟它的质量成正比，g=，G=mg。（g=9.8N/g）

  • 重力与质量的区别和联系：
    质量 重力
    区别 概念 物体所含物质的多少 由于地球吸引而使物体受到的力
    符号 m G
    量性 只有大小，没有方向 既有大小，又有方向
    单位 千克（kg） 牛顿（N）
    与地理位置的关系 与位置无关 与位置有关
    公式 m=ρV G=mg
    测量工具 天平 测力计
    联系 重力与质量的关系是G=mg（g=9.8N/kg）

  • 重力加速度：
         重力加速度g的方向总是竖直向下的。在同一地区的同一高度，任何物体的重力加速度都是相同的。重力加速度的数值随海拔高度增大而减小。当物体距地面高度远远小于地球半径时，g变化不大。而离地面高度较大时，重力加速度g数值显著减小，此时不能认为g为常数。
         距离地面同一高度的重力加速度，也会随着纬度的升高而变大。由于重力是万有引力的一个分力，万有引力的另一个分力提供了物体绕地轴作圆周运动所需要的向心力。物体所处的地理位置纬度越高，圆周运动轨道半径越小，需要的向心力也越小，重力将随之增大，重力加速度也变大。地理南北两极处的圆周运动轨道半径为0，需要的向心力也为0，重力等于万有引力，此时的重力加速度也达到最大。
http://www.00-edu.com/html/202004/59198.html十二生肖
十二星座