下列说法中错误的是（）A．如果杠杆的阻力臂和动力臂之比是2：1，杠杆的阻力大小为100N，那么，要是杠杆平衡必须施加200N的动力B．距井底0.2m深的水下，受到水的压强为200PaC．用-物理打印页面

下列说法中错误的是（）A．如果杠杆的阻力臂和动力臂之比是2：1，杠杆的阻力大小为100N，那么，要是杠杆平衡必须施加200N的动力B．距井底0.2m深的水下，受到水的压强为200PaC．用-物理

[db:作者] 2020-04-23 00:00:00 零零社区

题文

下列说法中错误的是（　　）
A．如果杠杆的阻力臂和动力臂之比是2：1，杠杆的阻力大小为100N，那么，要是杠杆平衡必须施加200N的动力
B．距井底0.2m深的水下，受到水的压强为200Pa
C．用300N的力推动重2000N的小车前进2m，重力做功是0
D．重为20N的木块在水中所受的浮力无法计算
题型：单选题难度：偏易

答案

A、杠杆的阻力臂和动力臂之比是2：1，即
L2
L1
=
2
1
，杠杆的阻力大小为100N，根据杠杆的平衡条件F₁×L₁=F₂×L₂得
F1
F2
=
L2
L1
=
2
1
，因此动力F₁=2F₂=200N，故该选项说法正确，但不符合题意．
B、水的深度是水中某点距水面的距离，距井底0.2m深的位置水深多少未知，因此液体压强无法求得，故该选项说法错误，符合题意．
C、重力的方向竖直向下，小车前进2m的距离是在水平方向上，不符合做功的要求，因此重力没有做功，故该选项说法正确，但不符合题意．
D、木块重力虽然知道，但是木块是漂浮在水面上还是在水中下沉未知，因此浮力无法计算，故该选项说法正确，但不符合题意．
故选B．

据专家权威分析，试题“下列说法中错误的是（）A．如果杠杆的阻力臂和动力臂之比是2：1，杠杆..”主要考查你对液体压强的计算，浮力及阿基米德原理，功的计算，杠杆的平衡条件等考点的理解。关于这些考点的“档案”如下：

液体压强的计算浮力及阿基米德原理功的计算杠杆的平衡条件

考点名称：液体压强的计算

液体压强的计算公式：
P=ρgh（ρ是液体密度，单位是千克/米³；g=9.8牛/千克；h是深度，指液体自由液面到液体内部某点的竖直距离，单位是米。）
对液体压强公式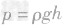的理解
1．由公式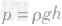可知，液体内部的压强只跟液体的密度和深度有关，而跟液体的质量、重力、体积以及容器的形状、底面积等无关。

2．公式只适用于计算静止的液体产生的压强，而对固体、气体或流动的液体均不适用。

3．在液体压强公式中h表示深度，而不是高度。判断出h的大小是计算液体压强的关键，如图所示，甲图中A点的深度为30cm，乙图中B点的深度为 40cm．丙图中C点的深度为50cm。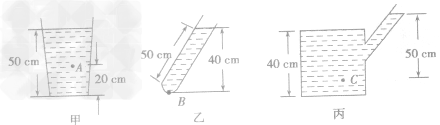

4．运用公式时应统一单位：ρ的单位用kg／m³，h 的单位用m，计算出的压强单位才是Pa。

5．两公式的区别与联系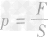：是压强的定义式，无论固体、液体还是气体，它都是普遍适用的；而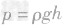是结合液体的具体情况通过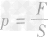推导出来的，所以适用于液体。

6．用公式求出的压强是液体由于自身重力产生的压强，它不包括液体受到的外加压强。

转换法和控制变量法探究液体压强大小跟哪些因素有关：
在探究液体压强的大小时，由于液体压强的大小不易测量或是不能直接观测到它的大小，我们用“转换法”，通过液体压强计中两玻璃管液面的高度差的大小来比较液体压强的大小，将抽象的东西变成了直观且形象的东两，使问题简化了。

由于液体内部压强跟液体的深度和液体密度两方面因素有关，所以在探究液体内部压强的规律时要采用控制变量法，即在探究液体压强与深度的关系时，要保持液体密度不变，在探究液体压强与液体的密度关系时，要保持液体的深度不变。

考点名称：浮力及阿基米德原理

浮力：
（1）定义：浸在液体中的物体受到向上托的力叫做浮力。
（2）施力物体与受力物体：浮力的施力物体是液体 (或气体)，受力物体是浸入液体(或气体)中的物体。
（3）方向：浮力的方向总是竖直向上的。
阿基米德原理：
（1）原理内容：浸在液体里的物体受到液体竖直向上的浮力，浮力的大小等于它排开的液体受到的重力。
（2）公式：，式中ρ_液表示液体的密度，V_排是被物体排开的液体的体积，g取9．8N／kg。
浮力大小跟哪些因素：
有关浸在液体中的物体受到浮力的大小，跟物体浸入液体中的体积有关，跟液体的密度有关，跟物体浸入液体中的深度无关。跟物体本身密度大小无关。
阿基米德原理的五点透析：
(1)原理中所说的“浸在液体里的物体”包含两种状态：一是物体的全部体积都浸入液体里，即物体浸没在液体里；二是物体的一部分体积浸入液体里，另一部分露在液面以上。

(2)G_排指被物体排开的液体所受的重力，F_浮= G_排表示物体受到的浮力的大小等于被物体排开的液体的重力。

(3)V_排是表示被物体排开的液体的体积，当物体全部浸没在液体里时，V_排=V_物；当物体只有一部分浸入液体里时，则V_排<V_物。

(4)由可以看出，浮力的大小只跟液体的密度和物体排开液体的体积这两个因素有关，而跟物体本身的体积、密度、形状、在液体中的深度、液体的多少等因素无关。

(5)阿基米德原理也适用于气体，但公式中ρ_液应该为ρ_气。

控制变量法探究影响浮力大小的因素:
     探究浮力的大小跟哪些因素有关时，用“控制变量法”的思想去分析和设计，具体采用“称量法”来进行探究，既能从弹簧测力计示数的变化中体验浮力，同时，还能准确地测出浮力的大小。
例1小明在生活中发现木块总浮在水面，铁块却沉入水底，因此他提出两个问题：
问题1：浸入水中的铁块是否受到浮力?
问题2：浮力大小与哪些因素有关?
为此他做了进一步的猜想，设计并完成了如图所示实验，
(1)(b)、(c)图中弹簧测力计示数均小于(a)图中弹簧测力计示数，说明浸入水中的铁块__(选填 “受到”或“不受到”)浮力；
(2)做___(选填字母)两次实验，是为了探究铁块浸没在水中时所受浮力大小与深度是否有关；
(3)做(d)、(e)两次实验，是为了探究浮力大小与 __的关系。

解析(1)物体在水中时受到水向上托的力，因此示数会变小。
(2)研究浮力与深度的关系时，应保持V_排和ρ_液不变，改变深度。
(3)在V_排不变时，改变ρ_液，发现浮力大小改变，说明浮力大小与ρ_液有关。
答案(1)受到(2)(c)、(d)(3)液体密度

公式法求浮力:
     公式法也称原理法，根据阿基米德原理，浸入液体中的物体受到向上的浮力，浮力的大小等于物体排开的液体受到的重力(表达式为：F_浮=G_排=ρ_液gV_排)。此方法适用于所有浮力的计算。
例1一个重6N的实心物体，用手拿着使它刚好浸没在水中，此时物体排开的水重是10N，则该物体受到的浮力大小为____N。
解析由阿基米德原理可知，F_浮=G_排=10N。
答案10

实验法探究阿基米德原理:
     探究阿基米德原理的实验，就是探究“浮力大小等于什么”的实验，结论是浮力的大小等于物体排开液体所受的重力。实验时，用重力差法求出物体所受浮力大小，用弹簧测力计测出排开液体重力的大小，最后把浮力与排开液体的重力相比较。实验过程中注意溢水杯中的液体达到溢口，以保证物体排开的液体全部流入小桶。
例1在探究“浮力大小等于什么”的实验中，小明同学的一次操作过程如图所示。

(1)测出铁块所受到的重力G铁；
(2)将水倒入溢水杯中；
(3)把铁块浸入溢水杯中，读出弹簧测力计示数F；
(4)测出小桶和被排开水的总重力G；
(5)记录分析数据，归纳总结实验结论，整理器材。
分析评估小明的实验，指出存在的问题并改正。
解析:在探究“浮力大小等于什么”的实验中，探究的结论是浮力的大小等于物体排开的液体所受到的重力，所以实验时，需要用弹簧测力计测出铁块受到的浮力和它排开水的重力进行比较得出结论，因此实验过程中需要测空小桶的重力G_桶，并且将溢水杯中的水加至溢水口处。
答案:存在的问题：
(1)没有测空小桶的重力 (2)溢水杯的水量不足
改正：(1)测空小桶的重力G_桶(2)将溢水杯中的水加至溢水口处
浮力知识梳理：
曹冲称象中的浮力知识：
   例曹冲利用浮力知识，巧妙地测出了大象的体重。请你写出他运用的与浮力有关的知识_____、 ____，另外，他所用到的科学研究方法是：_____和______.

   解析:曹冲称象的过程是首先把大象放在船上，在水面处的船舷上刻一条线，然后把大象牵上岸。再往船上放入石块，直到船下沉到船舷上的线再次与水面相平时为止，称出此时船上石头的质量即为大象的质量。两次船舷上的线与水面相平，根据阿基米德原理可知，为了让两次船排开水的体积相同，进而让两次的浮力相同，再根据浮沉条件，漂浮时重力等于浮力可知：船重+大象重=船重+石头重，用多块石头的质量替代了不可拆分的大象的质量，这是等效替代法在浮力中的一个典型应用。

   答案:浮沉条件阿基米德原理等效替代法化整为零法

考点名称：功的计算

功的计算公式：
功（W）等于力（F）跟物体在力的方向上通过的距离（s）的乘积。（功=力×距离），W=FS。

单位：
国际单位制中，力的单位是N，距离的单位是m，功的单位是N·m，它有一个专用名称叫做焦耳，简称焦，用符号J表示，1J=1N·m。
在利用该公式进行计算时的注意点：
(1)力与物体移动的距离在方向上必须一致；

(2)力与物体移动的距离必须对应于同一物体；

(3)力与物体移动的距离必须对应于同一段时间。

考点名称：杠杆的平衡条件

杠杆的平衡条件：
动力×动力臂=阻力×阻力臂。
即
在杠杆平衡时，动力臂是阻力臂的几倍，动力就是阻力的几分之几。
利用杠杆平衡条件来分析和计算有关问题，一般遵循以下步骤：
(1)确定杠杆支点的位置。
(2)分清杠杆受到的动力和阻力，明确其大小和方向，并尽可能地作出力的示意图。
(3)确定每个力的力臂。
(4)根据杠杆平衡条件列出关系式并分析求解。

例：如图所示，AOB为一机械设备的简化示意图，我们可以把它看成杠杆(自重不计)，已知AO= 2OB。固定D点，使OB处于水平位置，此时B端挂一重为40N的物体，要使杠杆不发生转动，至少需在A端施加F=____N的力，在图上画出此时力F的方向。

解析：要想得到施加在A点的最小力，就要找到最大力臂，由图可知，最大力臂应是OA，故过A点作们的垂线，方向斜向下即为最小力。据杠杆平衡条件得：F·OA=G·OB，代入数值为F×2OB=40N×OB，解方程得F=20N。
答案：20   力F的方向如图

实验法探究杠杆平衡条件：
    实验前要调节杠杆的平衡螺母使其在水平位置上平衡，目的是使杠杆的重心落在支点上，从而消除杠杆的重力对平衡的影响。当杠杆水平平衡时，O点距悬挂钩码处的距离便是力臂，而且可用杠杆上的“格数”代替力臂大小。

例：我们都做过“探究杠杆平衡条件”的实验。
(1)实验没有挂钩码时，若杠杆左端下倾，则应将右端的平衡螺母向____(选填“左”或“右”)调节，使杠杆在水平位置平衡。实验前使杠杆水平平衡的目的是____.
(2)实验中，用图所示的方式悬挂钩码，杠杆也能水平平衡(杠杆上每格等距)，但老师却提醒大家不要采用这种方式。这主要是因为该种方式(    )
A．一个人无法独立操作
B．需要使用太多的钩码
C．力臂与杠杆不重合
D．力和力臂数目过多
(3)图中，不改变支点O右侧所挂的两个钩码及其位置，保持左侧第____格的钩码不动，将左侧另外两个钩码改挂到它的下方，杠杆仍可以水平平衡。

解析：(1)实验前要调节杠杆的平衡螺母使其在水平位置平衡，目的是方便地测量力臂。调节方法是将平衡螺母向杠杆偏高的一端调，即哪端轻向哪端调。
(2)探究杠杆平衡条件时，用的力和力臂数目过多，每个力都会给杠杆转动带来影响，给探究过程带来麻烦。
(3)根据杠杆平衡条件，即，所以l₁=2(格)。

答案：(1)右方便地测量力臂(2)D(3)2

利用杠杆平衡条件求最小力的方法:
    由公式可知，当阻力、阻力臂一定时，动力臂越长，动力越小。当动力臂最长时，动力最小。要求最小动力，必须先画出最大动力臂。
1．寻找最大动力臂的方法
(1)当动力作用点确定后，支点到动力作用点的线段即为最大动力臂；
(2)动力作用点没有规定时，应看杠杆上哪一点离支点最远，则这一点到支点的距离即为最大动力臂。
2．作最小动力的方法
(1)找到最大动力臂后，过作用点作动力臂的垂线；
(2)根据实际，动力能使杠杆沿阻力作用的反方向转动，从而确定动力的方向。

http://www.00-edu.com/html/202004/59508.html十二生肖
十二星座