如图所示装置中，杠杆和滑轮的重力及滑轮的摩擦均可忽略不计，杠杆AB可以绕O点在竖直平面内自由转动，A端通过竖直方向的轻绳与滑轮组相连，在B端用一轻绳沿竖直方向将杠杆拉-九年级物理打印页面

如图所示装置中，杠杆和滑轮的重力及滑轮的摩擦均可忽略不计，杠杆AB可以绕O点在竖直平面内自由转动，A端通过竖直方向的轻绳与滑轮组相连，在B端用一轻绳沿竖直方向将杠杆拉-九年级物理

[db:作者] 2020-04-22 00:00:00 互联网

题文

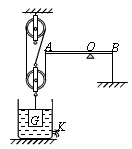
如图所示装置中，杠杆和滑轮的重力及滑轮的摩擦均可忽略不计，杠杆AB可以绕O点在竖直平面内自由转动，A端通过竖直方向的轻绳与滑轮组相连，在B端用一轻绳沿竖直方向将杠杆拉住，使其始终保持水平平衡。在滑轮组的下方，悬挂一圆柱形的物体，此物体被浸在圆柱形容器内的液体中。已知杠杆O点两侧的长度关系为AO=2OB，圆柱形物体的底面积为10cm²、高为12cm，圆柱形容器的底面积为50cm²。若容器中的液体为水，在水深为20cm时物体的上表面恰与水面相平，此时杠杆B端绳上的拉力为F₁；打开圆柱形容器下方的阀门K，将水向外释放，直到物体露出水面的体积为其总体积的2/3时，将阀门K关闭，此时杠杆B端绳上的拉力为F₂，且F₁ ：F₂=3：5。若容器中液体为某种未知液体，其质量与最初容器中的水的质量相等，此时未知液体的深度为18 cm，杠杆B端绳上的拉力为F₃。（取g=10N/kg）求：
（1）圆柱形物体的密度；
（2）未知液体的密度；
（3）作用在B端的拉力F₃大小；（小数点后保留两位）
（4）未知液体对圆柱形容器底部的压强。

题型：计算题难度：偏难

答案

（1）2 g/cm³；
（2）1.1 g/cm³ ；
（3）为0.87N ；
（4）1980Pa

据专家权威分析，试题“如图所示装置中，杠杆和滑轮的重力及滑轮的摩擦均可忽略不计，杠..”主要考查你对液体压强计算公式的应用，液体压强的计算，浮力及阿基米德原理，密度的计算，二力平衡的定义及条件等考点的理解。关于这些考点的“档案”如下：

液体压强计算公式的应用液体压强的计算浮力及阿基米德原理密度的计算二力平衡的定义及条件

考点名称：液体压强计算公式的应用

利用液体压强的计算公式计算：ρ、h。
液体压强中隐含“密度不同”的有关计算：
由液体的压强公式可知，液体的压强大小取决于液体的密度和深度，深度的不同比较直观，一眼可以看到，而密度不同需引起注意，有时直接给出物质不同，密度不同，有时则隐含着密度不同，需要自己发现。
例如图所示，两支相同的试管，内盛等质量的液体，甲管竖直放置，乙管倾斜放置，液体对管底压强的大小关系是（）

A．p甲<p乙
B．p甲>p乙
C．p甲=p乙
D．上述三种情况都有可能
解析:比较压强就从甲、乙两支试管中液体的密度和深度分析。依据题意已知h相等，因此本题只要比较出甲、乙管中液体的密度ρ，即可判断出正确答案。由质量关系已知，要比较密度很容易想到密度公式，从而转向寻找甲、乙两支试管中液体的体积关系，这样问题就得到了解决。由题意可知，两试管液面相平，高度相等，虽然两试管中所装的液体质量相等，但乙管倾斜放置，，所以，据可知。
答案:B

液体对容器底的压力与液体的重力
1．由于液体具有流动性，静止在水平放置的容器中的液体，对容器底的压力不一定等于液体的重力。只有当容器是柱形时，容器底的压力才等于液体的重力：底小口大的容器底受到的压力小于液体的重力；底大口小的容器底受到的压力大于液体的重力。液体对容器底的压力F=pS=ρghS，而Sh的含义是以容器底为底、以液体深度为高的柱体的体积。即V_柱=Sh，所以F=pS=ρghS=，G_柱的含义为以V_柱为体积的那部分液体的重力，如图中阴影部分。即若容器为柱体，则F=G_液；若容器为非柱体，则。

2．在盛有液体的容器中，液体对容器底的压力、压强遵循液体的压力、压强规律；而容器对水平桌面的压力、压强遵循固体的压力、压强规律。
例：在水平桌面上放置一空玻璃杯，它的底面积为0．01m²，它对桌面的压强为200Pa。
(1)求玻璃杯的重力。
(2)在玻璃杯中装入1kg水后，水对杯底产，￡的压强为900Pa，求水的深度；并通过计算推测出玻璃杯的大致形状是图中甲、乙、丙的哪一种?(水的密度p= 1．0×103k/m³，取g=10N／kg，杯壁的厚度可忽略)

解析：
（1）由得：玻璃杯的重力：
（2）由得水的深度：
假设杯壁是竖直的，装入1KG水后杯中水的深度应为：，因为h'>h，所以水杯底小，口大，大致形状是甲图。

液体对容器底的压强、压力与容器对支持面的压强、压力的计算方法：
液体对容器底的压强和压力与容器对支持面的压强和压力不是一同事。
1．液体内部压强是由液体的重力产生的，但液体对容器底的压力并不一定等于液体的重力，而等于底面积所受的压强乘以受力面积，因此，处理液体内部问题时，先求压强再算压力。
2．容器对支持面的压力和压强，可视为固体问题处理，先分析压力大小，再根据计算压强大小。
例：如图所示，一开口的杯子，装上8cm高的水后，放在水平桌面上。已知杯子内部底面积为50cm²，外部底面积为60cm²；杯子装上水后的总质量为 0．6kg，则水对杯底的压力为___N，杯子对桌面的压强为_____Pa.

解析：从杯子的形状可知，杯中水对杯底的压力并小等于水的重力，要求液体对容器底的压力时，一般是先求出压强，再根据F=pS求压力，即F=pS=10^-3m²=4N，而杯子对桌面的压力为杯与水的总重，即，压强。
答案：4N 1×10³

考点名称：液体压强的计算

液体压强的计算公式：
P=ρgh（ρ是液体密度，单位是千克/米³；g=9.8牛/千克；h是深度，指液体自由液面到液体内部某点的竖直距离，单位是米。）
对液体压强公式的理解
1．由公式可知，液体内部的压强只跟液体的密度和深度有关，而跟液体的质量、重力、体积以及容器的形状、底面积等无关。

2．公式只适用于计算静止的液体产生的压强，而对固体、气体或流动的液体均不适用。

3．在液体压强公式中h表示深度，而不是高度。判断出h的大小是计算液体压强的关键，如图所示，甲图中A点的深度为30cm，乙图中B点的深度为 40cm．丙图中C点的深度为50cm。

4．运用公式时应统一单位：ρ的单位用kg／m³，h 的单位用m，计算出的压强单位才是Pa。

5．两公式的区别与联系：是压强的定义式，无论固体、液体还是气体，它都是普遍适用的；而是结合液体的具体情况通过推导出来的，所以适用于液体。

6．用公式求出的压强是液体由于自身重力产生的压强，它不包括液体受到的外加压强。

转换法和控制变量法探究液体压强大小跟哪些因素有关：
在探究液体压强的大小时，由于液体压强的大小不易测量或是不能直接观测到它的大小，我们用“转换法”，通过液体压强计中两玻璃管液面的高度差的大小来比较液体压强的大小，将抽象的东西变成了直观且形象的东两，使问题简化了。

由于液体内部压强跟液体的深度和液体密度两方面因素有关，所以在探究液体内部压强的规律时要采用控制变量法，即在探究液体压强与深度的关系时，要保持液体密度不变，在探究液体压强与液体的密度关系时，要保持液体的深度不变。

考点名称：浮力及阿基米德原理

浮力：
（1）定义：浸在液体中的物体受到向上托的力叫做浮力。
（2）施力物体与受力物体：浮力的施力物体是液体 (或气体)，受力物体是浸入液体(或气体)中的物体。
（3）方向：浮力的方向总是竖直向上的。
阿基米德原理：
（1）原理内容：浸在液体里的物体受到液体竖直向上的浮力，浮力的大小等于它排开的液体受到的重力。
（2）公式：，式中ρ_液表示液体的密度，V_排是被物体排开的液体的体积，g取9．8N／kg。
浮力大小跟哪些因素：
有关浸在液体中的物体受到浮力的大小，跟物体浸入液体中的体积有关，跟液体的密度有关，跟物体浸入液体中的深度无关。跟物体本身密度大小无关。
阿基米德原理的五点透析：
(1)原理中所说的“浸在液体里的物体”包含两种状态：一是物体的全部体积都浸入液体里，即物体浸没在液体里；二是物体的一部分体积浸入液体里，另一部分露在液面以上。

(2)G_排指被物体排开的液体所受的重力，F_浮= G_排表示物体受到的浮力的大小等于被物体排开的液体的重力。

(3)V_排是表示被物体排开的液体的体积，当物体全部浸没在液体里时，V_排=V_物；当物体只有一部分浸入液体里时，则V_排<V_物。

(4)由可以看出，浮力的大小只跟液体的密度和物体排开液体的体积这两个因素有关，而跟物体本身的体积、密度、形状、在液体中的深度、液体的多少等因素无关。

(5)阿基米德原理也适用于气体，但公式中ρ_液应该为ρ_气。

控制变量法探究影响浮力大小的因素:
     探究浮力的大小跟哪些因素有关时，用“控制变量法”的思想去分析和设计，具体采用“称量法”来进行探究，既能从弹簧测力计示数的变化中体验浮力，同时，还能准确地测出浮力的大小。
例1小明在生活中发现木块总浮在水面，铁块却沉入水底，因此他提出两个问题：
问题1：浸入水中的铁块是否受到浮力?
问题2：浮力大小与哪些因素有关?
为此他做了进一步的猜想，设计并完成了如图所示实验，
(1)(b)、(c)图中弹簧测力计示数均小于(a)图中弹簧测力计示数，说明浸入水中的铁块__(选填 “受到”或“不受到”)浮力；
(2)做___(选填字母)两次实验，是为了探究铁块浸没在水中时所受浮力大小与深度是否有关；
(3)做(d)、(e)两次实验，是为了探究浮力大小与 __的关系。

解析(1)物体在水中时受到水向上托的力，因此示数会变小。
(2)研究浮力与深度的关系时，应保持V_排和ρ_液不变，改变深度。
(3)在V_排不变时，改变ρ_液，发现浮力大小改变，说明浮力大小与ρ_液有关。
答案(1)受到(2)(c)、(d)(3)液体密度

公式法求浮力:
     公式法也称原理法，根据阿基米德原理，浸入液体中的物体受到向上的浮力，浮力的大小等于物体排开的液体受到的重力(表达式为：F_浮=G_排=ρ_液gV_排)。此方法适用于所有浮力的计算。
例1一个重6N的实心物体，用手拿着使它刚好浸没在水中，此时物体排开的水重是10N，则该物体受到的浮力大小为____N。
解析由阿基米德原理可知，F_浮=G_排=10N。
答案10

实验法探究阿基米德原理:
     探究阿基米德原理的实验，就是探究“浮力大小等于什么”的实验，结论是浮力的大小等于物体排开液体所受的重力。实验时，用重力差法求出物体所受浮力大小，用弹簧测力计测出排开液体重力的大小，最后把浮力与排开液体的重力相比较。实验过程中注意溢水杯中的液体达到溢口，以保证物体排开的液体全部流入小桶。
例1在探究“浮力大小等于什么”的实验中，小明同学的一次操作过程如图所示。

(1)测出铁块所受到的重力G铁；
(2)将水倒入溢水杯中；
(3)把铁块浸入溢水杯中，读出弹簧测力计示数F；
(4)测出小桶和被排开水的总重力G；
(5)记录分析数据，归纳总结实验结论，整理器材。
分析评估小明的实验，指出存在的问题并改正。
解析:在探究“浮力大小等于什么”的实验中，探究的结论是浮力的大小等于物体排开的液体所受到的重力，所以实验时，需要用弹簧测力计测出铁块受到的浮力和它排开水的重力进行比较得出结论，因此实验过程中需要测空小桶的重力G_桶，并且将溢水杯中的水加至溢水口处。
答案:存在的问题：
(1)没有测空小桶的重力 (2)溢水杯的水量不足
改正：(1)测空小桶的重力G_桶(2)将溢水杯中的水加至溢水口处
浮力知识梳理：
曹冲称象中的浮力知识：
   例曹冲利用浮力知识，巧妙地测出了大象的体重。请你写出他运用的与浮力有关的知识_____、 ____，另外，他所用到的科学研究方法是：_____和______.

   解析:曹冲称象的过程是首先把大象放在船上，在水面处的船舷上刻一条线，然后把大象牵上岸。再往船上放入石块，直到船下沉到船舷上的线再次与水面相平时为止，称出此时船上石头的质量即为大象的质量。两次船舷上的线与水面相平，根据阿基米德原理可知，为了让两次船排开水的体积相同，进而让两次的浮力相同，再根据浮沉条件，漂浮时重力等于浮力可知：船重+大象重=船重+石头重，用多块石头的质量替代了不可拆分的大象的质量，这是等效替代法在浮力中的一个典型应用。

   答案:浮沉条件阿基米德原理等效替代法化整为零法

考点名称：密度的计算

公式：
密度的公式：ρ=m/V(ρ表示密度、m表示质量、V表示体积)

密度公式变化：m=ρV、V=m/ρ
正确理解密度公式：
理解密度公式时，要注意条件和每个物理量所表示的特殊含义。从数学的角度看有三种情况（判断正误）：

1. 同种物质:
（1）ρ一定时，m和V成正比；（因为ρ=m/V，ρ一定，m增大，V也增大，所以成正比）
（2）m一定时，ρ与V成反比；（因为m=ρv,m一定，v增大，ρ变小，所以成反比）
（3）V一定时，ρ与m成正比。
结合物理意义，三种情况只有（1）的说法正确，（2）（3）都是错误的。
因为同种物质的密度是一定的，它不随体积和质量的变化而变化，所以在理解物理公式时，不可能脱离物理事实，不能单纯地从数学的角度理解物理公式中各量的关系。

2. 不同物质:
（1）具有不同物质的物体，在体积相同的情况下，密度大的质量也大，物体的质量跟它的密度成正比；
（2）具有不同物质的物体，在质量相同的条件下，密度大的体积反而小，物体的体积跟它的密度成反比。

考点名称：二力平衡的定义及条件

定义:
物体在两个力作用下保持静止或匀速直线运动状态，我们就说这两个力平衡.
二力平衡的条件：
同物：两个力作用在同一物体上
等值：两个力大小相等
反向：两个力方向相反
共线：两个力在同一直线上

说明：
①二力平衡时要求四个条件同时具备，缺一不可。
②判断二力是否平衡既可用二力平衡条件来判断，也可根据物体是否处于平衡状态来确定受到的力是否平衡
隐含“二力平衡”的变形题：
    考查二力平衡与平衡状态的试题很多，形式变化多样，有一些条件很直接，而有时具有隐蔽性，但始终遵循平衡力和平衡状态的对应关系，准确把握这一关系，适应多变题型。题型多以填空题、选择题的形式出现。
例:如图所示，各用4N的水平力沿相反的方向拉弹簧测力计的两端(弹簧测力计自重不计)，则下列说法中正确的是(   )

A．弹簧测力计的示数为4N，弹簧测力计受的合力为4N
B．弹簧测力计的示数为0N，弹簧测力计受的合力为0N
C．弹簧测力计的示数为8N，弹簧测力计受的合力为0N
D．弹簧测力计的示数为4N，弹簧测力计受的合力为0N
解析:本题考查弹簧测力计的原理，弹簧测力计是利用力产生的效果大小来测量力的大小的。弹簧测力计的构造是弹簧一端固定(与挂环相连的一端)，叫做固定端；另一端与挂钩相连，叫做自由端。测量时，使固定端不动，拉力拉挂钩使弹簧伸长，拉力越大，弹簧伸长就越长，弹簧测力计的示数就越大，也就是说，弹簧测力计指针的示数等于作用在挂钩上的拉力的大小，是一端的力的大小，而不是两端的受力之和所以在本题中弹簧测力计的示数是4N。而把弹簧测力计作为研究对象，在一对平衡力作用下，合力是零。
答案：D

二力平衡的判断方法：
    判断一对力是否是平衡力，有两种方法。一种是根据二力平衡条件判断，只要两个力“同体、等大、反向、共线”，那么，这两个力就是一对平衡力。另一种是根据物体的运动状态是否改变判断，如果物体在某一方向上受到一对力而运动状态保持不变，那么这一对力就是平衡力，反之，就不是平衡力。
例1一本物理书静止在水平桌面七，下列各对力中属于平衡力的是（）
A．书对地球的引力和地球对书的引力
B．书受到的重力和桌面对书的支持力
C．书对桌面的压力和书受到的重力
D．书对桌面的压力和桌面对书的支持力
解析：互为平衡力的两个力应满足：受力物体相同，大小相等，方向相反，作用在同一条直线上。A 项中的两个力的受力物体不同，是一对相互作用力；B 项重力和支持力四个条件都符合，是平衡力；C项中的两个力不满足受力物体相同和方向相反的条件，不是平衡力；D项中的两个力的受力物体不同，施力物体和受力物体刚好相反，是一对相互作用力。
答案：B
二力平衡的意义：
二力平衡是力的分析的最简单、最基本的情况，若一物体处于二力平衡状态，我们了解了其中一个力，对另一个力也就了如指掌。如图所示，一物体放在水平桌面上，它将受到重力和桌面对它的支持力，物体处于平衡状态。我们知道了物体的重力，根据等大、反向、共线的关系，也就知道了支持力，的大小、方向及作用点。

二力平衡的作用效果：
二力平衡的效果不仅使物体保持平衡状态，还使物体发生了形变(只不过有时效果不明显，但形变还是有的，如静止在地面上的物体受重力和地面支持力的作用，发生了微小形变)。因此，两个力并不是完全抵消而没有产生任何力的作用效果。

补充：
(1)物体在两平衡力作用下处于平衡状态，若再加一对或多对平衡力，物体将仍然处于平衡状态。
(2)平衡力可以通过受力图形象地描绘出来。

二力平衡的应用：
（1）用弹簧测力计测量物体所受重力时，就是利用二力平衡条件。
（2）放在桌面上的花瓶受到竖直向下的重力和桌面对他竖直向上的支持力，二力平衡。
（3）悬挂着的吊灯，受到竖直向下的重力和吊线对它竖直向上的拉力，二力平衡。
（4）在水平道路上匀速直线运动的汽车，水平方向受到向前的牵引力和向后的阻力，二力平衡。
（5）在竖直方向，汽车受到向下的重力和路面对它向上的支持力，二力平衡。

http://www.00-edu.com/html/202004/57066.html十二生肖
十二星座