零零教育信息网 首页 > 考试 > 物理 > 初中物理 > 压强的大小及其计算 > 正文 返回　打印

用油罐车运输煤油．油罐的容积为6m3，空油罐车的质量为7200kg，装满煤油后车轮与地面的总接触面积为O.2m2．油罐车在水平路面上匀速行驶9000m，发动机牵引力所做的功为1.8×10-物理
[db:作者]  2020-05-27 00:00:00  互联网

题文

用油罐车运输煤油．油罐的容积为6m3，空油罐车的质量为7200kg，装满煤油后车轮与地面的总接触面积为O.2m2．油罐车在水平路面上匀速行驶9000m，发动机牵引力所做的功为1.8×107J．煤油的密度为O．8×103kg/m3．g取10N/kg．试求：
（1）油罐中最多能装多少千克的煤油？
（2）装满煤油的油罐车对地面的压强是多少？
（3）油罐车在水平路面上匀速行驶时，发动机的牵引力是多少？
题型：问答题  难度：中档

答案

（1）煤油的质量
m1=ρV=0.8×103kg/m3×6m3=4.8×103kg．
答：油罐中最多能装4.8×103kg的煤油．
（2）装满煤油的油罐车对地面的压力F=G=（m1+m2）g=（4.8×103kg+7.2×103kg）×10N/kg=1.2×105N．
装满煤油的油罐车对地面的压强是P=
F
S
1.2×105N
0.2m2
=6×105Pa．
答：装满煤油的油罐车对地面的压强是6×105Pa．
（3）因为W=Fs
所以F=
W
S
=
1.8×107J
9000m
=2×103N．
答：油罐车在水平路面上匀速行驶时，发动机的牵引力是2×103N．

据专家权威分析，试题“用油罐车运输煤油．油罐的容积为6m3，空油罐车的质量为7200kg，装..”主要考查你对  压强的大小及其计算，功的计算，密度的计算，密度公式的应用，二力平衡的定义及条件  等考点的理解。关于这些考点的“档案”如下：

压强的大小及其计算功的计算密度的计算密度公式的应用二力平衡的定义及条件

考点名称：压强的大小及其计算

  • 计算公式：
    P=F/S，式中p单位是：帕斯卡，简称：帕，1帕=1牛/米2，压力F单位是：牛；受力面积S单位是：米2。

  • 对压强公式的理解：
    1．此公式适用于任何情况，即固体、液体、气体的压强计算都可用此公式。

    2．此公式中各物理量单位分别是p→Pa、F→N、s→m2。在计算物体的压强时，只有当F的单位为N，S 的单位为m2时，压强的单位才能是Pa，因此在计算中必须统一单位。

    3．一张报纸平放时对桌子的压强约0．5Pa。成人站立时对地面的压强约为1．5×104Pa，它表示：人站立时，其脚下每平方米面积上，受到脚的压力为1．5× 104N。

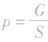    4．公式中的，是压力而不是重力。即使在某些情况下，压力在数值上等于物体所受的重力，也不应把公式直接写成，而应先注明F=G得：。

    5．公式中的受力面积S，是指受力物体发生形变的那部分面积，也就是两物体的实际接触面积，而不一定是受力物体的表面积。如图所示，一个圆台形物体置于水平地面上，分别采用A、B两种方式放置，对地面的压力不变，但图A中受力面积是S2，图B中受力面积为S1，而它们都与水平地面的面积大小无关。

    6.  由公式推导出F=pS和可用于计算压力和受力面积的大小。

    巧用求柱体压强：
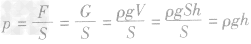      将一密度均匀、高为h的圆柱体放在水平桌面上，桌面受到的压强，所圆柱体(包括长方体、正方体等)产生的压强，只与固体的密度和高度有关，而与固体的重力、体积和底面积因素无关，应用公式就给解这类题带来很大方便。
    例1如图所示，两圆柱形铁柱的底面半径之比是 3：1，高度相同，则它们对水平地面的压强之比为（   ）

    A．3：1B．1：3C．1：1D．9：l
    解析：本题是分析圆柱体的压强，可直接利用公式进行分析。因为两圆柱体的密度相同、高度相同，所以压强相同，选项C正确。
    答案：C

考点名称：功的计算

  • 功的计算公式：
    功（W）等于力（F）跟物体在力的方向上通过的距离（s）的乘积。（功=力×距离），W=FS。

    单位：
    国际单位制中，力的单位是N，距离的单位是m，功的单位是N·m，它有一个专用名称叫做焦耳，简称焦，用符号J表示，1J=1N·m。

  • 在利用该公式进行计算时的注意点：
    (1)力与物体移动的距离在方向上必须一致；

    (2)力与物体移动的距离必须对应于同一物体；

    (3)力与物体移动的距离必须对应于同一段时间。

考点名称：密度的计算

  • 公式：
    密度的公式：ρ=m/V(ρ表示密度、m表示质量、V表示体积)

    密度公式变化：m=ρV、V=m/ρ

  • 正确理解密度公式：
    理解密度公式时，要注意条件和每个物理量所表示的特殊含义。从数学的角度看有三种情况（判断正误）：

    1. 同种物质:
    （1）ρ一定时，m和V成正比；（因为ρ=m/V，ρ一定，m增大，V也增大，所以成正比）
    （2）m一定时，ρ与V成反比；（因为m=ρv,m一定，v增大，ρ变小，所以成反比）
    （3）V一定时，ρ与m成正比。
    结合物理意义，三种情况只有（1）的说法正确，（2）（3）都是错误的。
    因为同种物质的密度是一定的，它不随体积和质量的变化而变化，所以在理解物理公式时，不可能脱离物理事实，不能单纯地从数学的角度理解物理公式中各量的关系。

    2. 不同物质:
    （1）具有不同物质的物体，在体积相同的情况下，密度大的质量也大，物体的质量跟它的密度成正比；
    （2）具有不同物质的物体，在质量相同的条件下，密度大的体积反而小，物体的体积跟它的密度成反比。

考点名称：密度公式的应用

  • 密度公式的应用：
    （1）利用m=ρV求质量；利用V=m/ρ求体积

    （2）对于密度公式，还要从以下四个方面理解
    ①同种物质，在一定状态下密度是定值，它不随质量大小或体积大小的改变而改变。当其质量（或体积）增大几倍时，其体积（或质量）也随着增大几倍，而比值是不变的。因此，不能认为物质的密度与质量成正比，与体积成反比；
    ②具有同种物质的物体，在同一状态下，体积大的质量也大，物体的体积跟它的质量成正比；
    ③具有不同物质的物体，在体积相同的情况下，密度大的质量也大，物体的质量跟它的密度成正比；

    ④具有不同物质的物体，在质量相同的条件下，密度大的体积反而小，物体的体积跟它的密度成反比。

  • 密度公式的应用：
    1. 有关密度的图像问题
    此问题一般是给出质量一体积图像，判断或比较物质密度。解答时可在横坐标(或纵坐标)任选一数值，然后在纵坐标(或横坐标)上找到对应的数值，进行分析比较。
     例1如图所示，是甲、乙两种物质的m一V图像，由图像可知(   )
    A．ρ甲>ρ乙
    B．ρ甲=ρ乙
    C．ρ甲<ρ乙
    D．无法确定甲、乙密度的大小

    解析:要从图像直接看出甲、乙两种物质的密度大小目前还做不到，我们要先借助图像，根据公式ρ =总结规律后方可。
    如图所示，在横轴上任取一点V0，由V0作横轴的垂线V0B，分别交甲、乙两图线于A、B两点，再分别从A、B两点作纵轴垂线，分别交纵轴于m甲、m乙两点。则甲、乙两种物质的密度分别为，ρ乙= ，因为m甲<m乙，所以ρ甲<ρ乙，故C正确。

    2. 密度公式ρ =及变形、m=ρV的应用：
    密度的公式是ρ =，可得出质量计算式m=ρV 和体积计算式。只要知道其中两个物理量，就可以代入相应的计算式进行计算。审题时注意什么量是不变的，什么量是变化的。
    例2某瓶氧气的密度是5kg/m3，给人供氧用去了氧气质量的一半，则瓶内剩余氧气的密度是_____；容积是10L的瓶子装满了煤油，已知煤油的密度是 0．8×103kg/m3，则瓶内煤油的质量是_____，将煤油倒去4kg后，瓶内剩余煤油的密度是______。
     解析：氧气用去一半，剩余部分仍然充满整个氧气瓶，即质量减半体积不变，所以氧气的密度变为 2．5kg/m3。煤油倒去一半后，体积质量同时减半，密度不变。
    答案：2．5kg/m3；8kg；0．8×10kg/m3。

    3. 比例法求解物质的密度
       利用数学的比例式来解决物理问题的方法称之为 “比例法”。能用比例法解答的物理问题具备的条件是：题目所描述的物理现象，由初始状态到终结状态的过程中至少有一个量保持不变，这个不变的量是由初始状态变成终结状态的桥梁，我们称之为“中介量”。
    例3甲、乙丽个物体的质量之比为3：2，体积之比为l：3，那么它们的密度之比为(   )
    A．1：2B．2：1C．2：9D．9：2
    解析：（1）写出所求物理量的表达式：，
    （2）写出该物理量比的表达式：

    （3）化简：代入已知比值的求解：


    密度、质量、体积计算中的“隐含条件” 问题：
      很多物理问题中的有些条件需要仔细审题才能确定，这类条件称为隐含条件。因此寻找隐含条件是解决这类问题的关键。以密度知识为例，密度计算题形式多样，变化灵活，但其中有一些题具有这样的特点：即质量、体积、密度中的某个量在其他量发生变化时保持不变，抓住这一特点，就掌握了求解这类题的规律。

    1．隐含体积不变
    例1一个瓶子最多能装0．5kg的水，它最多能装_____kg的水银，最多能装_____m3的酒精。 ρ水银=13．6×103kg／m3，ρ水=1．0×103kg／m3，ρ酒精= 0．8×103kg／m3)
    解析:最多能装即装满瓶子，由最多装水量可求得瓶子的容积为V=5×10-4m3，则装水银为m水银=13．6×103kg／m3×5×10-4m3=6．8kg。装酒精的体积为瓶子的容积。
    答案6．8；5×10-4

    2. 隐含密度不变
    例2一块石碑的体积为V样=30m3，为测石碑的质量，先取了一块刻制石碑时剔下来的小石块作为样品，其质量是m样=140g，将它放入V1=100cm3的水中后水面升高，总体积增大到V2=150cm3，求这块石碑的质量m碑。
    解析：此题中隐含的条件是石碑和样品是同种物质，密度相同，而不同的是它们的体积和质量。依题意可知，样品体积为：
    V样=V2-V1=150cm3一100cm3=50cm3 =5．0×10-5m3
    得=84t
    答案：84t

    3. 隐含质量不变
    例3质量为450g的水结成冰后，其体积变化了 ____m3。(ρ水=0．9×103kg／m3)
    解析：水结成冰后，密度减小，450g水的体积为，水结成冰后，质量不变，因此冰的体积为=500cm3=5．0×10-4m3，=5．0× 10-4m3一4．5×10-4m3=5×10-5m3。

    合金物体密度的相关计算：
         首先要抓住合金体的总质量与总体积分别等于各种物质的质量之和与体积之和这一特征，然后根据具体问题，灵活求解。
    例两种不同的金属，密度分别为ρ1、ρ2：
    (1)若墩质量相等的金属混合后制成合金，则合金的密度为____。
    (2)若取体积相等的金属混合后制成合金，则合金的密度为_____。
    解析：这道题的关键是抓住“两总”不变，即总质量和总体积不变。在(1)中，两种金属的质量相等，设为m1=m2=m，合金的质量m总=2m，则密度为ρ1的金属的体积V1=，密度为ρ2的金属的体积V2=，合金的体积，则合金的密度
    在（2）中两种金属的体积相等，设为，合金的体积，密度为ρ1的金属的质量m1=，密度为ρ2的金属的质量为，合金的质量m总，合金的密度为。
    答案：
    注意：上述规律也适用于两种液体的混合，只要混合液的总质量和总体积不变即可。

考点名称：二力平衡的定义及条件

  • 定义:
    物体在两个力作用下保持静止或匀速直线运动状态，我们就说这两个力平衡.

  • 二力平衡的条件：
    同物：两个力作用在同一物体上
    等值：两个力大小相等
    反向：两个力方向相反
    共线：两个力在同一直线上

    说明：
    ①二力平衡时要求四个条件同时具备，缺一不可。
    ②判断二力是否平衡既可用二力平衡条件来判断，也可根据物体是否处于平衡状态来确定受到的力是否平衡

  • 隐含“二力平衡”的变形题：
        考查二力平衡与平衡状态的试题很多，形式变化多样，有一些条件很直接，而有时具有隐蔽性，但始终遵循平衡力和平衡状态的对应关系，准确把握这一关系，适应多变题型。题型多以填空题、选择题的形式出现。
    例:如图所示，各用4N的水平力沿相反的方向拉弹簧测力计的两端(弹簧测力计自重不计)，则下列说法中正确的是(   )

    A．弹簧测力计的示数为4N，弹簧测力计受的合力为4N
    B．弹簧测力计的示数为0N，弹簧测力计受的合力为0N
    C．弹簧测力计的示数为8N，弹簧测力计受的合力为0N
    D．弹簧测力计的示数为4N，弹簧测力计受的合力为0N
    解析:本题考查弹簧测力计的原理，弹簧测力计是利用力产生的效果大小来测量力的大小的。弹簧测力计的构造是弹簧一端固定(与挂环相连的一端)，叫做固定端；另一端与挂钩相连，叫做自由端。测量时，使固定端不动，拉力拉挂钩使弹簧伸长，拉力越大，弹簧伸长就越长，弹簧测力计的示数就越大，也就是说，弹簧测力计指针的示数等于作用在挂钩上的拉力的大小，是一端的力的大小，而不是两端的受力之和所以在本题中弹簧测力计的示数是4N。而把弹簧测力计作为研究对象，在一对平衡力作用下，合力是零。
    答案：D

    二力平衡的判断方法：
        判断一对力是否是平衡力，有两种方法。一种是根据二力平衡条件判断，只要两个力“同体、等大、反向、共线”，那么，这两个力就是一对平衡力。另一种是根据物体的运动状态是否改变判断，如果物体在某一方向上受到一对力而运动状态保持不变，那么这一对力就是平衡力，反之，就不是平衡力。
    例1一本物理书静止在水平桌面七，下列各对力中属于平衡力的是（）
    A．书对地球的引力和地球对书的引力
    B．书受到的重力和桌面对书的支持力
    C．书对桌面的压力和书受到的重力
    D．书对桌面的压力和桌面对书的支持力
    解析：互为平衡力的两个力应满足：受力物体相同，大小相等，方向相反，作用在同一条直线上。A 项中的两个力的受力物体不同，是一对相互作用力；B 项重力和支持力四个条件都符合，是平衡力；C项中的两个力不满足受力物体相同和方向相反的条件，不是平衡力；D项中的两个力的受力物体不同，施力物体和受力物体刚好相反，是一对相互作用力。
    答案：B

  • 二力平衡的意义：
        二力平衡是力的分析的最简单、最基本的情况，若一物体处于二力平衡状态，我们了解了其中一个力，对另一个力也就了如指掌。如图所示，一物体放在水平桌面上，它将受到重力和桌面对它的支持力，物体处于平衡状态。我们知道了物体的重力，根据等大、反向、共线的关系，也就知道了支持力，的大小、方向及作用点。

    二力平衡的作用效果：
        二力平衡的效果不仅使物体保持平衡状态，还使物体发生了形变(只不过有时效果不明显，但形变还是有的，如静止在地面上的物体受重力和地面支持力的作用，发生了微小形变)。因此，两个力并不是完全抵消而没有产生任何力的作用效果。

    补充：
    (1)物体在两平衡力作用下处于平衡状态，若再加一对或多对平衡力，物体将仍然处于平衡状态。
    (2)平衡力可以通过受力图形象地描绘出来。

    二力平衡的应用：
    （1）用弹簧测力计测量物体所受重力时，就是利用二力平衡条件。
    （2）放在桌面上的花瓶受到竖直向下的重力和桌面对他竖直向上的支持力，二力平衡。
    （3）悬挂着的吊灯，受到竖直向下的重力和吊线对它竖直向上的拉力，二力平衡。
    （4）在水平道路上匀速直线运动的汽车，水平方向受到向前的牵引力和向后的阻力，二力平衡。
    （5）在竖直方向，汽车受到向下的重力和路面对它向上的支持力，二力平衡。
http://www.00-edu.com/html/202005/63158.html十二生肖
十二星座