 |
首页 > 考试 > 物理 > 初中物理 > 压强的大小及其计算 > 正文 | 返回 打印 |
|
 |
首页 > 考试 > 物理 > 初中物理 > 压强的大小及其计算 > 正文 | 返回 打印 |
|
答案
 模型1即为甲杯:由于ρ1<ρ2,两种液体的质量且各占一半.可得密度ρ1的液体体积大于密度ρ2的液体,密度ρ1的液体体积用灰标记,密度ρ2的液体体积用蓝色标记. 模型2即为乙杯:两种液体体积相等,密度ρ1的液体体积用灰标记,密度ρ2的液体体积用蓝色标记. 对照组体现体积相等时之间的分界线. 对模型1密度ρ1的液体体积进行处理,切割成和模型2中密度ρ1的液体体积相同,即是容器体积的一半(如图所示).对模型2中密度ρ2的液体体积进行处理,切割成和模型1中密度ρ2的液体体积相同(如图所示),经过处理便可以直接从对比处比较甲、乙两杯内液体质量的大小 了,答案很明显是对比处是蓝色的乙杯大.所以液体对乙杯底的压力大. 故选B. |
据专家权威分析,试题“现有密度分别为ρ1和ρ2的两种液体,且ρ1<ρ2,在甲杯中盛满这两种液..”主要考查你对 压强的大小及其计算,密度公式的应用 等考点的理解。关于这些考点的“档案”如下:
压强的大小及其计算密度公式的应用
考点名称:压强的大小及其计算
 的理解:
的理解: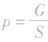 ,而应先注明F=G得:
,而应先注明F=G得: 。
。 
 可用于计算压力和受力面积的大小。
可用于计算压力和受力面积的大小。 求柱体压强:
求柱体压强: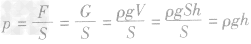 ,所圆柱体(包括长方体、正方体等)产生的压强,只与固体的密度和高度有关,而与固体的重力、体积和底面积因素无关,应用公式
,所圆柱体(包括长方体、正方体等)产生的压强,只与固体的密度和高度有关,而与固体的重力、体积和底面积因素无关,应用公式 就给解这类题带来很大方便。
就给解这类题带来很大方便。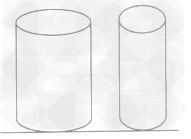
 进行分析。因为两圆柱体的密度相同、高度相同,所以压强相同,选项C正确。
进行分析。因为两圆柱体的密度相同、高度相同,所以压强相同,选项C正确。考点名称:密度公式的应用
密度公式的应用:
(1)利用m=ρV求质量;利用V=m/ρ求体积
(2)对于密度公式,还要从以下四个方面理解
①同种物质,在一定状态下密度是定值,它不随质量大小或体积大小的改变而改变。当其质量(或体积)增大几倍时,其体积(或质量)也随着增大几倍,而比值是不变的。因此,不能认为物质的密度与质量成正比,与体积成反比;
②具有同种物质的物体,在同一状态下,体积大的质量也大,物体的体积跟它的质量成正比;
③具有不同物质的物体,在体积相同的情况下,密度大的质量也大,物体的质量跟它的密度成正比 ;
;
④具有不同物质的物体,在质量相同的条件下,密度大的体积反而小,物体的体积跟它的密度成反比 。
。

 总结规律后方可。
总结规律后方可。 ,ρ乙=
,ρ乙=  ,因为m甲<m乙,所以ρ甲<ρ乙,故C正确。
,因为m甲<m乙,所以ρ甲<ρ乙,故C正确。
 及变形
及变形 、m=ρV的应用:
、m=ρV的应用: ,可得出质量计算式m=ρV 和体积计算式
,可得出质量计算式m=ρV 和体积计算式 。只要知道其中两个物理量,就可以代入相应的计算式进行计算。审题时注意什么量是不变的,什么量是变化的。
。只要知道其中两个物理量,就可以代入相应的计算式进行计算。审题时注意什么量是不变的,什么量是变化的。 ,
,


 =84t
=84t ,水结成冰后,质量不变,因此冰的体积为
,水结成冰后,质量不变,因此冰的体积为 =500cm3=5.0×10-4m3,
=500cm3=5.0×10-4m3, =5.0× 10-4m3一4.5×10-4m3=5×10-5m3。
=5.0× 10-4m3一4.5×10-4m3=5×10-5m3。 ,密度为ρ2的金属的体积V2=
,密度为ρ2的金属的体积V2= ,合金的体积
,合金的体积 ,则合金的密度
,则合金的密度
 ,合金的体积
,合金的体积 ,密度为ρ1的金属的质量m1=
,密度为ρ1的金属的质量m1= ,密度为ρ2的金属的质量为
,密度为ρ2的金属的质量为 ,合金的质量m总
,合金的质量m总 ,合金的密度为
,合金的密度为 。
。