 |
首页 > 考试 > 物理 > 初中物理 > 功率的计算 > 正文 | 返回 打印 |
|
|
首页 > 考试 > 物理 > 初中物理 > 功率的计算 > 正文 | 返回 打印 |
|
答案
| 已知：m1=5t=5000kg，m2=1.25t=1250kg，L1=AO=10m，g=10N/kg，h=4m，t=20s，W额=3×104J 求：L2，P有用，η （1）F1=G1=m1g=5000kg×10N/kg=5×104N， F2=G2=m2g=1250kg×10N/kg=1.25×104N， 根据杠杆平衡条件：F1L1=F2L2 C离O点的距离L2=
（2）W有用=G2h=1.25×104N×4m=5×104J， P有用=
η=
答：（1）C应移动到离O点40m远的地方； （2）“塔吊”提升水泥板的功率是2.5×103W；“塔吊”的机械效率为62.5%． |
据专家权威分析，试题““塔吊”是建筑工地上常见的起重设备，在汶川地震灾区救援现场，用..”主要考查你对 功率的计算，机械效率的计算，杠杆的动态平衡分析 等考点的理解。关于这些考点的“档案”如下：
功率的计算机械效率的计算杠杆的动态平衡分析
考点名称：功率的计算
公式法计算功率：
运用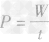
时一定要注意三个量的对应关系。“W”一定是对应“t”完成的，不能张冠李戴。单位要统一，P、W、t的单位分别为瓦、焦、秒。
例1 如图所示，铁明同学向上跳台阶进行晨练，铁明重500N，在10s内匀速连跳12个台阶，每个台阶的高度为0．2m。在这个过程中，已知铁明克服摩擦做功为2800J，求出此过程中：
(1)铁明竖直向上跳的平均速率多大?
(2)铁明克服重力做功是多少?
(3)铁明做功的总功率多大?
解析：竖直向上跳的平均速度可以通过向上跳的总高度与所用时间利用速度公式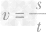
求出，克服重力做功等于重力与高度的乘积，即
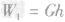，总功率可以通过所做的总功和时间利用功率公式
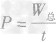求得。
（1）
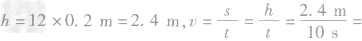0.24m/s
（2）
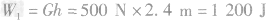
（3）
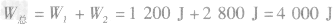
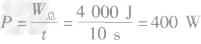
例2在打捞海底沉船时，常用水下机器人潜入水下打捞船上物品，已知ρ海水=1．03×103kg／m3。
(1)机器人在水下70m处受到海水产生的压强是多大?
(2)某时刻机器人在水下用竖直向上的力举着体积为0.02m3，密度为2.7×103kg/m3的物体静止不动，求该力的大小。
(3)若机器人在水下运动时，所受海水阻力与速度的关系如图所示，求机器人在水下以0．5m／s的水平速度匀速运动时，机器人水平推进力的功率。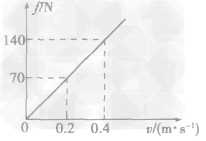
解析：（1）由液体压强公式
得，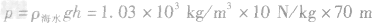
，
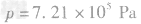
（2）物体在水下受平衡力的作用，则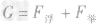
则
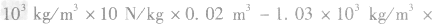
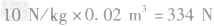
（3）由题图可知，海水阻力与机器人的运动速度成正比，当机器人运动速度为0．5m/s时，f=175N 机器人匀速前进时，机器人水平推进力F=f
P=Fv=175N×0．5m/s=87．5W
答案：（1）7.21×105Pa（2）334N（3）87.5W
考点名称：机械效率的计算
| 物理量 | 物理意义 | 定义 | 符号 | 公式 | 单位 | 说明 |
| 功 | 做功即能量的转化 | 有力作用在物体上，并且物体在力的方向上移动了一段距离，就说力对物体做了功 | W | W=Fs | J | l. 功率大小由功和时间共同决定，单独强调某一方面是错误的 2．功率和机械效率是两个不同的物理量，它们之问没有直接关系 |
| 功率 | 做功快慢 | 单位时间内完成的功 | P |  |
W(国际单位) kW，MW（常用单位） | |
| 机械效率 | 反映机械性能的物理量 | 有用功占总功的总值 | η |  |
无 |
考点名称：杠杆的动态平衡分析
杠杆的平衡状态：
杠杆静止不动或匀速转动都叫做杠杆平衡，注意我们在实验室所做的杠杆平衡条件的实验，是在杠杆水平位置平衡进行的，但在实际生产和生活中，这样的平衡是不多的，在许多情况下，杠杆是倾斜静止的，这是因为杠杆受到平衡力作用。所以说杠杆不论处于怎样的静止，都可以理解成处于平衡状态。
杠杆动态平衡问题：
杠杆动态平衡的几种类型杠杆动态平衡是指构成杠杆的某些要素发生变化,而杠杆仍处于静止状态或匀速转动状态，
分析杠杆的动态平衡时，一般是动中取静，根据杠杆平衡条件，分析比较，得出结论。下面就杠杆动态平衡问题归类分析。
一、 阻力一定，判断动力的变化情况
1、l1不变，l2变化
例1、如图1所示，轻质杠杆可绕O转动，在A点始终受一垂直作用于杠杆的力，在从A转动A/位置时，力F将（）
A、变大
B、变小
C、先变大，后变小
D、先变小，后变大 
分析：当杠杆在水平面以下上升到水平面上时，l1不变，l2增大，由
，F增大，当杠杆从水平面继续上升过程中，l2减小，所以F减小。
2、l2不变，l1变化
例2、如图2所示，轻质杠杆OA的B点挂着一个重物，A端用细绳吊在圆环M下，此时OA恰成水平且A点与圆弧形架PQ的圆心重合，那么当环M从P点逐渐滑至Q点的过程中，绳对A端的拉力大小将（）
A、保持不变
B、逐渐增大
C、逐渐减小
D、由大变小再变大 
分析：当M点从P点滑至Q点的过程中，我们分两个过程分析，
一是从P点滑至竖直位置，动力臂l1逐渐增大（同学们不妨作出这两点的动力臂），由
知F逐渐变小；
二是从竖直位置到Q点，动力臂逐渐减小，所以又逐渐增大。故选D。
3、l1与l2同时变化，但比值不变
例3、用图3所示的杠杆提升重物，设作用在A端的力F始终竖直向下，在将重物慢慢提升到一定高度的过程中，F的大小将（）
A、保持不变
B、逐渐变小
C、逐渐变大
D、先变大，后变小 
分析：：F始终竖直向下，与阻力作用线平行，分别作出F与G的力臂l1和l2，构建两个相似三角形（同学们不妨在图中作出），可以看出，
为定值，由杠杆平衡条件，
，得
，所以，F大小不变。
4、l1与l2同时变化
例4、如图4所示，一个直杠杆可绕轴O转动，在直杆的中点挂一重物，在杆的另一端施加一个方向始终保持水平的力F，将直杆从竖直位置慢慢抬起到水平位置过程中，力F大小的变化情况是（）
A、一直增大
B、一直减小
C、先增大后减小
D、先减小后增大
分析：将直杆从竖直位置慢慢抬起到水平位置过程中，l1变小，l2变大，由
知，F一直在增大。
二、动力与阻力不变，动力臂与阻力臂变化
例5、如图5所示，用一细线悬挂一根粗细均匀的轻质细麦桔杆，使其静止在水平方向上， O为麦桔杆的中点．这时有两只蚂蚁同时从O点分别向着麦桔杆的两端匀速爬行，在蚂蚁爬行的过程中麦桔杆在水平方向始终保持乎衡，则（）
A、两蚂蚁的质量一定相等
B、两蚂蚁的爬行速度大小一定相等
C、两蚂蚁的质量与爬行速度大小的乘积一定相等
D、两蚂蚁对麦桔杆的压力一定相等 
分析：蚂蚁爬行的过程中麦桔杆始终保持乎衡，有
，即
，所以
。故选C。
三、动力臂与阻力臂不变，动力与阻力改变
例6、如图6所示的轻质杠杆，AO小于BO．在A、B两端悬挂重物（同种物质）G1和G2后杠杆平衡．若将G1和G2同时浸没到水中则（）
A、杠杆仍保持平衡
B、杠杆的A端向下倾斜
C、杠杆的B端向下倾斜
D、无法判断
分析：在空气中，杠杆平衡，故有
；G1和G2同时浸没到水中，有
，说明杠杆仍然平衡。故选A。
