题目
随着人们生活水平的提高．轿车已逐步进入我国普通百姓家中。已知某国产骄车每行驶100km消耗8L汽油(1L＝10-3 m3)，汽油的密度为0.71×103kg/m3、热值为4.6×107J／kg。则
（1）10kg汽油完全燃烧时所产生的热量是_________J．
（2）该汽车行驶100km消耗的汽油的质量是________kg．
（3）当该汽车以50kW的功率在平直公路上以72km／h的速度匀速行驶时，它所受到的阻力等于____N。 |
题型：填空题难度：偏易来源：同步题
所属题型：填空题
试题难度系数：偏易
答案
考点梳理
初中二年级物理试题“随着人们生活水平的提高．轿车已逐步进入我国普通百姓家中。已知某”旨在考查同学们对
热值、
功率的计算公式的应用、
密度公式的应用、
……等知识点的掌握情况，关于物理的核心考点解析如下：
此练习题为精华试题，现在没时间做？添加到收藏夹，以后再看。
根据试题考点，只列出了部分最相关的知识点，更多知识点请访问初二物理。
考点名称：热值
热值：热值指某种燃料完全燃烧放出的热量与其质量之比，是一种物质特定的性质。单位是J/kg或J/m^3(气体)。
(1)燃料的热值与燃料的种类有关，热值反映的是所有能燃烧的物质的一种性质，也就是说它是燃料的一种特性，反映了不同燃料在燃烧过程中，化学能转化为内能的本领的大小。燃料的热值只与燃料的种类有关，与燃料的形态、质量、体积以及是否完全燃烧无关。
(2)“完全燃烧”的含义是烧完、烧尽，1kg的某种燃料，只有在完全燃烧的情况下，放出的热量才等于这种燃料的热值，若该燃料在燃烧时没有完全燃烧，放出的热量就比对应的热值小。
燃料热值计算公式
固体燃料完全燃烧释放的热量的计算公式：Q放=mq，气体燃料完全燃烧释放的热量的计算公式：Q=Vq Q表示热量(J)，q表示热值( J/kg )，m表示固体燃料的质量(kg)，V表示气体燃料的体积(m^3)。
q=Q放/m(固体);q=Q放/v(气体)
W=Q放=qm=Q放/m W=Q放=qV=Q放/v (W：总功)(热值与压强有关)
SI制国际单位： Q———某种燃料完全燃烧后放出的热量———焦耳 J
m———表示某种燃料的质量———千克 kg
q———表示某种燃料的热值———焦耳每千克 J/kg
热值的单位换算
燃料及其燃烧的关系
能够燃烧并且在燃料时放出光和热的物质，叫做燃料。
燃料的燃烧是一种化学变化，在燃烧的过程中，燃料的化学能转化为内能，这就是我们常说的释放能量，然后，转移到其他物体上或转化为其他形式的能量供人们使用.
说明：按照状态，燃料可分为固体燃料(如煤、炭、木材等)、液体燃料(如汽油、煤油、石油等)和气体燃料(如天然气、煤气、沼气等)。
考点名称：功率的计算公式的应用
单位时间里完成的，叫做功率，表示作功快慢程度的物理量，通常用P表示，故功率等于作用力与物体受力点速度的标量积。
功率的计算公式及单位
电功率计算公式：P=W/t =UI;在纯电阻电路中，根据欧姆定律U=IR代入P=UI中还可以得到：P=I²R=(U²)/R。
在动力学中：功率计算公式：1.P=W/t(平均功率)2.P=FV;P=Fvcosa(瞬时功率)
因为W=F(f力)×S(s位移)(功的定义式)，所以求功率的公式也可推导出P=F·v：P=W /t=F*S/t=F*V(此公式适用于物体做匀速直线运动)
功率单位为瓦特，简称“瓦”，符号是“W”。W表示功，单位是“焦耳”，简称“焦”，符号是“J”。“t”表示时间，单位是“秒”，符号是“s”。
功率计算公式的应用
例1：用杠杆来撬一重为2400 N的大石块，当手在5 s内用300 N的力按杠杆，将杠杆一端压下1.6 m，大石块被举高多少m?人做功的功率为多大?(不计杠杆的重力和摩擦)
思路导航：(1)解答此题的关键是能够想到功的原理，往往有同学会用杠杆原理来解答此题，存在这种错误的同学主要是没有正确理解什么是力臂，题中给出的1.6 m是动力沿动力的方向通过的距离，而不是动力臂，题中要求的大石块被举高的高度恰好就是阻力沿阻力方向通过的距离。人对杠杆做的功即动力对杠杆做的功W1=Fs=300 N×1.6 m=480 J(注意：F和s对应)，根据功的原理，W1=W2。
W2=G物h=2400 N×h. 480 J=2400×h，解得：h=0.2 m。
(2)人做功的功率就是动力做功的功率为96 W。
方法指导：利用杠杆做功时，在杠杆平衡的时候，根据功的原理和杠杆原理。
例2：关于功、功率，下列说法正确的是[ ]
A.机械的效率越高，做功越多
B.机械的效率越高，做功越快
C.机械的功率越大，做功越多
D.机械的功率越大，做功越快
思路导航：功率是表示做功的快慢，而不是做功多少的物理量；机械效率是表示有用功在总功中的比值，与做功的多少及功率的大小无关；所以本题的正确答案为D。
方法指导：这道题目包含了这章内容的三个重要的概念：功、功率、机械效率，只有真正理解了这些概念，才能准确的完成这道题。
例3：功率为30 kW，机械效率为60%的水泵，1 h内能把多少t的水从100 m深的矿井中抽到地面？（g取10 N/kg)
思路导航：本题既考查了功、功率、时间的关系，又考查了总功、有用功和机械效率的关系，利用水泵的功率，工作时间可以求出所做的总功W总=Pt，根据有用功、总功、机械效率的关系可以求出有用功W有=W总η，结合有用功的意义，在这里水泵对水所做的功就是有用功，即W有=G水h，这样就可以求出水的质量，解答过程如下：
W总=Pt=3×104 W×3600 s=1.8×108 J
W有=W总η=1.08×108 J×0.6=6.48×107 J（注意单位时统一）
W有=G水h
G水=6.48×105 N
m水=6.48×104 kg=64.8 t
方法指导：根据题中所给的已知条件来确定要选用的公式，同一个物理量可以通过好多途径来求，这就要求我们把学过的知识要能紧紧地联系在一起，做到灵活运用，融会贯通。
考点名称：密度公式的应用
密度换算公式：
密度的公式：ρ=m/V(ρ表示密度、m表示质量、V表示体积)
密度公式变化：m=ρV、V=m/ρ
正确理解密度公式：
理解密度公式时，要注意条件和每个物理量所表示的特殊含义。从数学的角度看有三种情况（判断正误）：
（1）ρ一定时，m和V成正比；（因为ρ=m/V，ρ一定，m增大，V也增大，所以成正比）
（2）m一定时，ρ与V成反比；（因为m=ρv,m一定，v增大，ρ变小，所以成反比）
（3）V一定时，ρ与m成正比。
结合物理意义，三种情况只有（1）的说法正确，（2）（3）都是错误的。
因为同种物质的密度是一定的，它不随体积和质量的变化而变化，所以在理解物理公式时，不可能脱离物理事实，不能单纯地从数学的角度理解物理公式中各量的关系。
常用气体密度换算：
1．干空气密度
密度是指单位体积空气所具有的质量, 国际单位为千克/米3（kg/m3 ），一般用符号ρ表示。其定义式为： ρ = M/V (1--1)
式中 M——空气的质量，kg；
V——空气的体积，m3。
空气密度随空气压力、温度及湿度而变化。上式只是定义式，通风工程中通常由气态方程求得干、湿空气密度的计算式。由气态方程有：
ρ=ρ0*T0*P/P0*T (1--2)
式中 ：ρ——其它状态下干空气的密度，kg/m3；
ρ0——标准状态下干空气的密度，kg/m3；
P、P0——分别为其它状态及标准状态下空气的压力，千帕（kpa）；
T、T0——分别为其它状态及标准状态下空气的热力学温度，K。
标准状态下，T0=273K，P0=101.3kPa时,组成成分正常的干空气的密度ρ0=1.293kg/m3。将这些数值代入式（1-2），即可得干空气密度计算式为：
ρ = 3.48*P/T(1--3)
使用上式计算干空气密度时，要注意压力、温度的取值。式中P为空气的绝对压力，单位为kPa；T为空气的热力学温度（K），T=273+t, t为空气的摄氏温度（℃）。
2．湿空气密度
对于湿空气，相当于压力为P的干空气被一部分压力为Ps的水蒸汽所占据，被占据后的湿空气就由压力为Pd的干空气和压力为Ps的水蒸汽组成。根据道尔顿分压定律，湿空气压力等于干空气分压Pd与水蒸汽分压Ps之和，即：P=Pd+Ps。
根据相对湿度计算式，水蒸汽分压Ps=ψPb，根据气态方程及道尔顿的分压定律，即可推导出湿空气密度计算式为：
ρw=3.48*P(1-0.378*ψ*Pb/P)/T (2--1)
式中 ρw ——湿空气密度,kg/m3；
ψ——空气相对湿度，%；
Pb——饱和水蒸汽压力，kPa(由表2-1-1确定)。
其它符号意义同上。
密度公式的应用：
1. 有关密度的图像问题
此问题一般是给出质量一体积图像，判断或比较物质密度。解答时可在横坐标(或纵坐标)任选一数值，然后在纵坐标(或横坐标)上找到对应的数值，进行分析比较。
例1如图所示，是甲、乙两种物质的m一V图像，由图像可知( )
A．ρ甲>ρ乙
B．ρ甲=ρ乙
C．ρ甲<ρ乙
D．无法确定甲、乙密度的大小
解析:要从图像直接看出甲、乙两种物质的密度大小目前还做不到，我们要先借助图像，根据公式ρ =
总结规律后方可。
如图所示，在横轴上任取一点V0，由V0作横轴的垂线V0B，分别交甲、乙两图线于A、B两点，再分别从A、B两点作纵轴垂线，分别交纵轴于m甲、m乙两点。则甲、乙两种物质的密度分别为
，ρ乙= 
，因为m甲<m乙，所以ρ甲<ρ乙，故C正确。
2. 密度公式ρ =及变形
、m=ρV的应用：
密度的公式是ρ =，可得出质量计算式m=ρV 和体积计算式。只要知道其中两个物理量，就可以代入相应的计算式进行计算。审题时注意什么量是不变的，什么量是变化的。
例2某瓶氧气的密度是5kg/m3，给人供氧用去了氧气质量的一半，则瓶内剩余氧气的密度是_____；容积是10L的瓶子装满了煤油，已知煤油的密度是 0．8×103kg/m3，则瓶内煤油的质量是_____，将煤油倒去4kg后，瓶内剩余煤油的密度是______。
解析：氧气用去一半，剩余部分仍然充满整个氧气瓶，即质量减半体积不变，所以氧气的密度变为 2．5kg/m3。煤油倒去一半后，体积质量同时减半，密度不变。
答案：2．5kg/m3；8kg；0．8×10kg/m3。
3. 比例法求解物质的密度
利用数学的比例式来解决物理问题的方法称之为 “比例法”。能用比例法解答的物理问题具备的条件是：题目所描述的物理现象，由初始状态到终结状态的过程中至少有一个量保持不变，这个不变的量是由初始状态变成终结状态的桥梁，我们称之为“中介量”。
例3甲、乙丽个物体的质量之比为3：2，体积之比为l：3，那么它们的密度之比为( )
A．1：2B．2：1C．2：9D．9：2
解析：（1）写出所求物理量的表达式：
，
（2）写出该物理量比的表达式：
（3）化简：代入已知比值的求解：
密度、质量、体积计算中的“隐含条件” 问题：
很多物理问题中的有些条件需要仔细审题才能确定，这类条件称为隐含条件。因此寻找隐含条件是解决这类问题的关键。以密度知识为例，密度计算题形式多样，变化灵活，但其中有一些题具有这样的特点：即质量、体积、密度中的某个量在其他量发生变化时保持不变，抓住这一特点，就掌握了求解这类题的规律。
1．隐含体积不变
例1一个瓶子最多能装0．5kg的水，它最多能装_____kg的水银，最多能装_____m3的酒精。 ρ水银=13．6×103kg／m3，ρ水=1．0×103kg／m3，ρ酒精= 0．8×103kg／m3)
解析:最多能装即装满瓶子，由最多装水量可求得瓶子的容积为V=5×10-4m3，则装水银为m水银=13．6×103kg／m3×5×10-4m3=6．8kg。装酒精的体积为瓶子的容积。
答案6．8；5×10-4
2. 隐含密度不变
例2一块石碑的体积为V样=30m3，为测石碑的质量，先取了一块刻制石碑时剔下来的小石块作为样品，其质量是m样=140g，将它放入V1=100cm3的水中后水面升高，总体积增大到V2=150cm3，求这块石碑的质量m碑。
解析：此题中隐含的条件是石碑和样品是同种物质，密度相同，而不同的是它们的体积和质量。依题意可知，样品体积为：
V样=V2-V1=150cm3一100cm3=50cm3 =5．0×10-5m3
得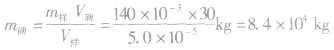
=84t
答案：84t
3. 隐含质量不变
例3质量为450g的水结成冰后，其体积变化了 ____m3。(ρ水=0．9×103kg／m3)
解析：水结成冰后，密度减小，450g水的体积为
，水结成冰后，质量不变，因此冰的体积为
=500cm3=5．0×10-4m3，
=5．0× 10-4m3一4．5×10-4m3=5×10-5m3。
合金物体密度的相关计算：
首先要抓住合金体的总质量与总体积分别等于各种物质的质量之和与体积之和这一特征，然后根据具体问题，灵活求解。
例两种不同的金属，密度分别为ρ1、ρ2：
(1)若墩质量相等的金属混合后制成合金，则合金的密度为____。
(2)若取体积相等的金属混合后制成合金，则合金的密度为_____。
解析：这道题的关键是抓住“两总”不变，即总质量和总体积不变。在(1)中，两种金属的质量相等，设为m1=m2=m，合金的质量m总=2m，则密度为ρ1的金属的体积V1=
，密度为ρ2的金属的体积V2=
，合金的体积
，则合金的密度
在（2）中两种金属的体积相等，设为
，合金的体积
，密度为ρ1的金属的质量m1=
，密度为ρ2的金属的质量为
，合金的质量m总
，合金的密度为
。
答案：
注意：上述规律也适用于两种液体的混合，只要混合液的总质量和总体积不变即可。
