题目
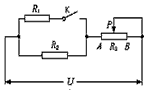
如图所示,R1=400Ω,R3的变阻范围是0~20Ω,电源电压U保持12V不变。
(1)当K断开、滑片P滑到B点时,电路消耗的总功率是1.2W,求R2的阻值;
(2)当K闭合、滑片P滑到A点时,求电路中每分钟释放的总热量。 |
 |
题型:计算题难度:偏难来源:模拟题
所属题型:计算题
试题难度系数:偏难
答案
解:(1)当K断开、滑片P滑到B点时,R1被断路,R2与R3串联。电路的总电流为:I= 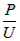 = =  =0.1AR3两端的电压为:U3=IR3=0.1A×20Ω=2V,R3两端的电压为:U2=U-U3=12V-2V=10V, =0.1AR3两端的电压为:U3=IR3=0.1A×20Ω=2V,R3两端的电压为:U2=U-U3=12V-2V=10V,
R2= 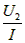 = = =100Ω。 =100Ω。
(2)当K闭合、滑片P滑到A点时,R1与R2并联,它们的总电阻为: R=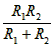 = = 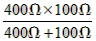 =80Ω, 电路中每分钟释放的总热量为: Q= =80Ω, 电路中每分钟释放的总热量为: Q= t= t=  ×60S=108J。 ×60S=108J。 |
考点梳理
初中三年级物理试题“如图所示,R1=400Ω,R3的变阻范围是0~20Ω,电源电压U保持12V不变”旨在考查同学们对
焦耳定律及计算公式、
电阻的并联、
欧姆定律及其应用、
电功率的计算公式的变形、
……等知识点的掌握情况,关于物理的核心考点解析如下:
此练习题为精华试题,现在没时间做?添加到收藏夹,以后再看。
根据试题考点,只列出了部分最相关的知识点,更多知识点请访问初三物理。
- 焦耳定律及计算公式
- 电阻的并联
- 欧姆定律及其应用
- 电功率的计算公式的变形
考点名称:焦耳定律及计算公式
焦耳的定律及公式:
焦耳定律或焦耳-冷次定律是定量说明传导电流将电能转换为热能的定律。1841年,英国物理学家詹姆斯·焦耳发现载流导体中产生的热量Q(称为焦耳热)与电流I的平方、导体的电阻R和通电时间t成比例。而在1842年时,俄国物理学家海因里希·楞次也独立发现上述的关系,因此也称为“焦耳-冷次定律”。
采用国际单位制时,焦耳定律的表达式为:
Q = I2Rt 或 P = I2R
其中Q(热量)、I(电流)、R(电阻)、t(时间)、P(热功率)各量的单位依次为焦耳、安培、欧姆、秒和瓦特。
焦耳定律是设计电照明,电热设备及计算各种电气设备温升的重要公式。
与欧姆定律的关系:
根据欧姆定律:
U=IR
焦耳定律的公式亦可表示为:

关于焦耳定律的历史:
关于导体中通过的电流与所产生的热量之间的定律。1840年由詹姆斯·普雷斯科特·焦耳提出。定律揭示了电流通过导线时所产生的热量和导线的电阻与电流平方的乘积成比例,即
H=0.24IRt
式中H 为产生的总热量,单位为卡;I 为电流,单位为安;R 为电阻,单位为欧;t为时间,单位为秒;0.24为由实验定出的比例常量。
焦耳是通过实验测定发现这个定律的。但是从理论上也不难理解,当电流的大小不变,产生的热量全部来源于电荷通过导体失去的势能。电荷的数量为It,失去的势能为W,W=RIt。因此,在单位时间中转变为热的电能为RI(焦),或者说在导体上消耗的电功率P为
P=RI(瓦)
焦耳定律是设计电照明,电热设备及计算各种电气设备温升的重要公式。
焦耳定律在串联电路中的运用:
在串联电路中,电流是相等的,则电阻越大时,产生的热越多。
焦耳定律在并联电路中的运用:
在并联电路中,电压是相等的,通过变形公式,W=Q=Pt=(U^2/R)×t,当U定时,R越大则Q越小。
需要注明的是,焦耳定律与电功公式W=UIt适任何元件及发热的计算,即只有在像电热器这样的电路(纯电阻电路)中才可用Q=W=UItq=I^2×Rt =(U^2/R)×t。
另外,焦耳定律还可变形为Q=IRq(后面的Q是电荷量,单位库仑(c))。
在热力学中指,气体的内能只是温度的函数,与体积无关。即内能对体积的偏导数为零。
考点名称:电阻的并联
电阻的并联:
并联电路总电阻的倒数等于各并联电阻的倒数之和。表达式:电阻R1R2R3……Rn并联,电压U1=U2=……=Un干路电流:In=I1+I2+……+In由于P=UI,I=U/R,代入,并联电阻的功率比P1:P2:P3……:Pn=U1^2/R1:U2^2/R2……Un^2/Rn=1/R1:R2……1/Rn由于是纯电阻,发热比Q1:Q2……:Qn=Pn比=1/R1:R2……1/Rn。
(1)把n个导体并联起来,相当于增加了导体的横截面积,其总电阻比每一个导体的电阻都要小。

串、并联电路中电流、电压、电阻的规律:

考点名称:欧姆定律及其应用
欧姆定律
欧姆定律是电学中的基本定律和核心内容,是贯穿整个电学的主线。在同一电路中,通过导体的电流跟导体两端的电压成正比,跟导体的电阻阻值成反比,这就是欧姆定律,基本公式是I=U/R,U表示导体两端的电压,单位是V;R表示导体的电阻,单位是Ω;I表示通过导体的电流,单位是A。
欧姆定律学习的重难点
1、要理解欧姆定律的内容
(1)欧姆定律中的关于成正比、成反比的结论是有条件的。如果说导体中的电流与导体两端的电压成正比,条件就是对于同一个电阻,也就是说在电阻不变的情况下;如果说导体中的电流与导体的电阻成反比,条件就是导体两端的电压不变。
(2)注意顺序,不能反过来说,电阻一定时,电压跟电流成正比。这里存在一个逻辑关系,电压是原因,电流是结果。是因为导体两端加了电压,导体中才有电流,不是因为导体中通了电流才有了电压,因果关系不能颠倒。同样也不能说导体的电阻与通过它的电流成反比。我们知道,电阻是导体本身的一种性质,即使导体中不通电流,它的电阻也不会改变,更不会因为导体中电流的增大或减小而使它的电阻发生改变。
2、要知道欧姆定律的公式和单位 欧姆定律的表达式I=U/R,可变形为U=IR和R=U/I,但这三个式子是有区别的。
(1)I=U/R,是欧姆定律的表达式,它反映了通过导体的电流的大小跟导体两端所加的电压这个外部原因和导体本身的电阻这个内部原因之间的因果关系。
(2)U=IR,当电流一定时,导体两端的电压跟它的电阻成正比。不能说成导体的电阻一定时导体两端的电压与通过的电流成正比,因为电压是形成电流的原因。电压的大小由电源决定,跟I、R无关,此式在计算比值时成立,不存在任何物理意义。
(3)R=U/I,此公式也是一个量变式,不存在任何物理意义。不能误认为导体的电阻跟导体两端的电压成正比,跟导体中的电流成反比。公式中的I、U、R都要用国际单位,即电流的单位为安培,符号A;电压的单位为伏特,符号V;电阻的单位为欧姆,符号Ω。
3.要明白定律的适用范围
(1)定律只适用于金属导电和液体导电,对于气体、半导体导电一般不适用。
(2)定律只适用于纯电阻电路。如:电路中只接有电阻器、电热器、白炽灯等用电器的电路。对于非纯电阻电路,如:电动机电路、日光灯电路等,则不能直接应用。
4.要理解欧姆定律的注意事项
(1)物理量的同一性。叙述欧姆定律时,在两个 “跟”字后面都强调了“这段导体”四个字,它是指对电路中同一导体或同一电路而言。所以在运用欧姆定律I=U/R等进行计算时,必须注意同一性,即I、R、U必须是 同一导体或同一段电路中的物理量。在表示I、U、R 时,注意脚标的一一对应。
(2)物理量的同时性。由于电路的连接方式发生改变,开关的断开或闭合,或滑动变阻器滑片的左右移动都可能使电路中总电阻发生变化,从而可能引起电路中电流和各部分电阻两端的电压发生变化。因此,必须注意在同一时刻、同一过程中的电压、电阻与电流的相互对应,不可将前后过程的I、R、U随意混用。
欧姆定律知识框架:

欧姆定律解题技巧
根据串、并联电路的特点和欧姆定律的公式可进行有关计算。
解题的方法是:
(1)根据题意画出电路图,看清电路的组成(串联还是并联);
(2)明确题目给出的已知条件与未知条件,并在电路图上标明;
(3)针对电路特点依据欧姆定律进行分析;
(4)列式解答。
考点名称:电功率的计算公式的变形
解读电功率的计算公式:
电功率的四个表达式:(1)定义式:P=W/t。(2)反映电学特点的普适式P=UI。与欧姆定律结合后得到的(3)式P=I2R。(4)式P=U2/R。
电功率是反映电能消耗快慢的物理量,定义为1秒钟内消耗电能的多少,因此,用所消耗的电能除以消耗这些电能所用的时间,就得到定义式P=W/t。
经实验研究证明,电功率等于导体两端电压与通过导体电流的乘积,即P=UI。电压和电流是电路中最重要的物理量。有电压才可能有电流。电能是通过电荷有规律的运动转化成其它形式的能量的,电荷有规律的运动就形成电流。没有电流就不会消耗电能,当然也就不会有电能转化为其它形式的能量。所以,P=UI广泛应用于电功率的计算。
与欧姆定律结合得到的(3)式P=I2R、(4)式P=U2/R适用于纯电阻电路。因为,欧姆定律反映的是导体中的电流与导体两端电压和导体电阻之间的关系,是在纯电阻电路中得出的,所以,它只适用于纯电阻电路。如:白炽灯、电阻、电热器等,不适用于含电动机的电路和输变电电路的计算。由于串联电路中电流处处相等,所以在串联电路中,使用(3)式P=I2R分析和计算方便。在并联电路中,各支路两端电压相等,所以用(4)式P=U2/R分析和计算方便。通过对近几年的中考命题分析,除了含电动机电路的电功率计算外,其它全是纯电阻电路。在纯电阻电路中,四个计算公式通用,可根据具体情况选择方便的公式进行运用。
电功率计算公式变形如下:
I=U/R
U=IR
R=U/I
P=W/T
P=UI
P=U^/R
P=I^R
Q=UIt 物理量 物理公式
电流 定义式I=Q/t 欧姆定律I=U/R 串联电路I=I1=I2 并联电路I=I1+I2
电压 串联电路U=U1+U2 并联电路U=U1=U2
电阻 串联R总=R1+R2 并联R总=R1R2/(R1+R2)
电功率 定义式P=W/t 普适公式P=UI
电功 定义式W=UIt 已知电功率W=Pt 已知电量W=UQ
导体热量 焦耳定律Q=I2Rt
面积 正方形S=a2 长方形S=ab 圆S=π(D/2)2
体积 柱体V=Sh 排液法V固=V2-V1 正方体V=a3 浸没时V排=V物
速度 定义式v=s/t 平均速度v=s总/t总
密度 定义式ρ=m/V
重力 G=mg
浮力 公式法F浮=ρ液gV排 称重法F浮=G-F' 漂浮和悬浮F浮=G 阿基米德原理F浮=G排
产生原因F浮=F向上-F向下 沉底时F浮=G-N
压强 定义式p=F/S 液体内部p=ρgh
功率(机械) 定义式P=W/t 汽车功率P=Fv
功(机械) 定义式W=Fs 总功W总=W有用+W额
杠杆平衡条件 F1l1=F2l2
力 同方向F合=F1+F2 反方向F合=F1-F2 水平桌面上受到物体的压力F=G总 液体、气体的压力F=pS
机械效率 定义式η=W有用/W总 提升重物η=Gh/Fs 水平移动重物η=fs物/Fs
热量 燃料燃烧Q=qm 物体吸放热Q=cmΔt
机械能 机械能=动能+势能
Q=U^/Rt
Q=I^Rt

