|
解:设试管中液体的密度为ρ0 ,内有密度为ρ( ρ>100)
体积为△V 的某种物质的微小颗粒,
则微小颗粒所受重力为G= ρ△Vg ,所受浮力为F= ρ0 △Vg
不计液体对微粒的粘滞阻力,微粒下沉的加速度为
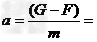 
当离心分离机带着试管绕竖直轴高速旋转时,试管几乎处于水平位置.如果试管中装着同一种液体,其液体密度为ρ0,这时试管中与转轴相距r、体积为△V的小液滴绕轴做圆周运动所需的向心力为F=ρ0△ω2r.这个向心力是周围的液体对该液滴作用的合力,若该处是体积为△V、密度为ρ(ρ>ρ0)的某种物质的微粒,它随离心分离机高速旋转时所需向心力为F′=ρ△Vω2r,然而周围液体对这个小微粒提供的作用力为F=ρ0△ω2r,由于ρ0<ρ,F<F′,即周围液体对微粒提供的作用力小于微粒所需的向心力,微粒便向管底“下沉”,沉淀加速度为a’=
假设液体中的物质微粒与转轴间距离r=0.2m,离心分离机的转速为3000r/min,则ω=314 rad/s,取g=10 m/s2,
可得  (倍) (倍)
可见,离心沉淀比 重力沉淀快得多 | 
