(1)传送带的速度
v的方向向右,大小为2.0 m/s.从速度图像中可以看出,物块被击穿后,先向左做减速运动,速度为零后,又向右做加速运动,当速度等于2 m/s以后随传送带一起向右做匀速运动.……………………………………………………………(2分)
(2)由速度图像可得,物块在滑动摩擦力的作用下做匀变速运动的加速度为
a,有
a=
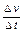
=

m/s
2="2.0" m/s
2………………………………………………………………(1分)
由牛顿第二定律:得
μMg=
Ma…………………………………………………………(2分)
得到物块与传送带间的动摩擦因数
μ=
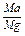
=

=0.2…………………………………………………………………………(1分)
(3)解法一:由速度图像可知,传送带与物块存在摩擦力的时间只有3秒,传送带在这段时间内移动的位移为
s,
s=
vt="2.0×3" m="6.0" m……………………………………………………………………(1分)
所以,传送带所做的功
W=
fs="4.0×6.0" J="24.0" J…………………………………………………………………(2分)
在物块获得速度到与传送带一起匀速运动的过程中,物块动能减少了Δ
EKΔ
EK=

-
 Mv2
Mv2=

×2.0×4
2-

×2.0×2
2="12.0" J……………………………………(1分)
所以转化的热能
EQ=
W+Δ
EK="24.0+12.0=36.0" J………………………………………(2分)
解法二:
以传送带为参考系,物块以相对于传送带的速度
v′=

+
v=4.0+2.0=6.0(m/s)……………………………………………………………(2分)
物块被击中后到相对静止的过程中,物块相对传送带通过的路程为:
s′=
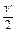 t
t=

×3=9(m)………………………………………………………………………(2分)
所以转化的热能
EQ=
fs′=4.0×9=36.0(J)……………………………………………(2分)

