如图12所示，水平平板小车质量为m=" 2kg," 其上左端放有一质量为M＝6kg的铁块，铁块与平板车间的动摩擦因数μ＝0.5，今二者以10m/s的速度向右运动，并与墙发生弹性碰撞，使小车以大小相同的速度反弹回，这样多次进行，求： ① 欲使M不从小车上落下，小车至少多长？ ② 第一次反弹后到最终状态，小车运动的总路程．（小车与水平面的摩擦不计，g=10m/s2 )
◎ 答案
（１）（２）
◎ 解析
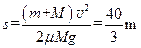
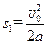
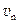
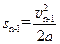
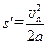
① 取平板车与铁块为研究系统，由M>m，系统每次与墙碰后m反向时，M仍以原来速度向右运动，系统总动量向右，故会多次反复与墙碰撞，每次碰后M都要相对m向右运动，直到二者停在墙边，碰撞不损失机械能，系统的动能全在M相对m滑动时转化为内能。设M相对m滑动的距离为s，则： 解得： 欲便M不从小车上落下，则L≥s，故平长 ② 小车第一次反弹向左以10m/s的速度做减速运动，直到速度为零，其加速度大小为 ( l 分） 故小车第一次向左的最大位移为，代入数据得 设小车第n-1次碰前速度为，第n次碰前速度为，则第n-1次碰后到第n次碰前过程动量守恒，有：，所以 第n－1次碰后小车反弹速度为，向左减速的最大位移为 随后向右加速距离为，显然，所以在碰前有相等速度 第n次碰后向左运动的最大位移(1分），所以 ，即成等比数列。小车运动的总路程为：
（２）
( l 分）
，代入数据得
，第n次碰前速度为
，则第n-1次碰后到第n次碰前过程动量守恒，有：
，所以
，显然
，所以在碰前有相等速度 
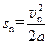
(1分），所以
，即成等比数列。小车运动的总路程为：