【错解分析】错解: 设甲与他的冰车以及乙与他的冰车的质量为M,箱子的质量为m,开始时他们的速率为v
0,为了不与乙相碰。
错解一:甲必须停止,所以,对甲和他的冰车及箱子,推出前后满足动量守恒,由动量守恒定律:
(M+m)v
0=0+mv

错解二:乙接到箱子后停下,所以,对箱子及乙和他的冰车,接到箱子前后动量守恒,设箱子的运动方向为正方向,由动量守恒定律有:
mv-Mv
0=0
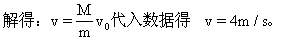
在此题中,有两个关键问题必须弄清楚,第一,“不相撞”的意义,是否意味着一个物体停下,实际上,不相撞的意义就是两个物体的速度相等(同向情况)。物体停止运动,也不一定就撞不上。如本题错解二。按照错解答案我们可知,当甲用4m/s的速度推箱子,箱子以4m/s的速度迎面向乙滑去,与乙相互作用后,乙与箱子都停下来了。那么,此时甲停了吗?我们可以继续完成本题,设甲推出箱子的速度为v',对甲和箱子,(以甲和箱子的初速度为正),由动量守恒定律有:
(M+m)v
0=Mv'+mv
解得:v'=1m/s。符号为正,说明甲以4m/s的速度推出箱子后继续向前运动,而乙接住箱子后要停下,这样甲就与乙相撞,所以4m/s的速度太小了。结果不符合题目要求。第二个关键在于不仅要不相撞,而且还要求甲推箱子的速度为最小,即若甲用相当大的速度推箱子,乙接到箱子后还会后退,这样就不满足“至少”多大的条件了,错解一即是这样,将所求的数据代入可以得知,乙和箱子将以0.67m/s的速度后退。
【正确解答】 要想刚好避免相撞,要求乙抓住箱子后与甲的速度正好相等,设甲推出箱子后的速度为v
1,箱子的速度为v,乙抓住箱子后的速度为v
2。
对甲和箱子,推箱子前后动量守恒,以初速度方向为正,由动量守恒定律:
(M+m)v
0= mv+Mv
1①
对乙和箱子,抓住箱子前后动量守恒,以箱子初速方向为正,由动量守恒定律有:
mv-Mv
0=(m+M)v
2②
刚好不相撞的条件是:
v
1="v" ③
联立①②③解得:v=5.2m/s,方向与甲和箱子初速一致。
【小结】 本题从动量守恒定律的应用角度看并不难,但需对两个物体的运动关系分析清楚(乙和箱子、甲的运动关系如何,才能不相撞)。这就需要我们要将“不相撞”的实际要求转化为物理条件,即:甲、乙可以同方向运动,但只要乙的速度不小于甲的速度,就不可能相撞。

