(11分)(2009·安徽省六校联考)如图所示，为某种新型设备内部电、磁场分布情况图．自上而下分为Ⅰ、Ⅱ、Ⅲ三个区域．区域Ⅰ宽度为d1，分布有沿纸面向下的匀强电场E1；区域Ⅱ宽度为d2，打印页面

(11分)(2009·安徽省六校联考)如图所示，为某种新型设备内部电、磁场分布情况图．自上而下分为Ⅰ、Ⅱ、Ⅲ三个区域．区域Ⅰ宽度为d1，分布有沿纸面向下的匀强电场E1；区域Ⅱ宽度为d2，

网友投稿 2023-04-12 00:00:00 零零社区

◎ 题目

(11分)(2009·安徽省六校联考)如图所示，为某种新型设备内部电、磁场分布情况图．自上而下分为Ⅰ、Ⅱ、Ⅲ三个区域．区域Ⅰ宽度为d1，分布有沿纸面向下的匀强电场E1；区域Ⅱ宽度为d2，分布有垂直纸面向里的匀强磁场B1；宽度可调的区域Ⅲ中分布有沿纸面向下的匀强电场E2和垂直纸面向里的匀强磁场B2.现在有一群质量和带电荷量均不同的带正电粒子从区域Ⅰ上边缘的注入孔A点被注入，从静止开始运动，然后相继进入Ⅱ、Ⅲ两个区域，满足一定条件的粒子将回到区域Ⅰ，其他粒子则从区域Ⅲ飞出．三区域都足够长，粒子的重力不计．
已知能飞回区域Ⅰ的带电粒子的质量为m＝6.4×10－27kg，带电荷量为q＝3.2×10－19C，且d1＝10cm，d2＝5cm，d3>10cm，E1＝E2＝40V/m，B1＝4×10－3T，B2＝2×10－3T.

试求：
(1)该带电粒子离开区域Ⅰ时的速度．
(2)该带电粒子离开区域Ⅱ时的速度．
(3)该带电粒子第一次回到区域Ⅰ的上边缘时离开A点的距离．

◎ 答案

　(1)2×104m/s　方向竖直向下
(2)2×104m/s　方向与x轴正向成45°角
(3)57.26cm

◎ 解析

(1)qE1d1＝mv2
得：v＝2×104m/s，方向竖直向下．
(2)速度大小仍为v＝2×104m/s，如图所示．
qB1v＝m
方向：sinθ＝
可得：θ＝45°
所以带电粒子离开区域Ⅱ时的速度方向与x轴正向成45°角．
(3)设该带电粒子离开区域Ⅱ也即进入区域Ⅲ时的速度分解为vx、vy，则：vx＝vy＝vsin45°＝×104m/s
所以：qB2vx＝qB2vy＝1.28×10－17N.
qE2＝1.28×10－17N
qE2＝qB2vx
所以带电粒子在区域Ⅲ中运动可视为沿x轴正向的速率为vx的匀速直线运动和以速率为vy，以及对应洛伦兹力qB2vy作为向心力的匀速圆周运动的叠加，轨道如图所示：

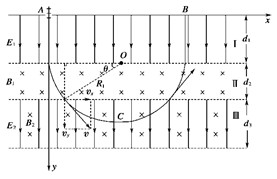
R2＝＝10cm
T＝＝π×10－5s
根据运动的对称性可知，带电粒子回到区域Ⅰ的上边缘的B点，距A点的距离为：d＝2
代入数据可得：d≈57.26cm

◎ 知识点

专家分析，试题“(11分)(2009·安徽省六校联考)如图所示，为某种新型设备内部电、磁场分布情况图．自上而下分为Ⅰ、Ⅱ、Ⅲ三个区域．区域Ⅰ宽度为d1，分布有沿纸面向下的匀强电场E1；区域Ⅱ宽度为d2，…”主要考查了你对【带电粒子在复合场中的运动】等知识点的理解和应用能力。关于这些知识点的“档案”，你可以点击相应的链接进行查看和学习。

http://www.00-edu.com/html/202304/444095.html十二生肖
十二星座