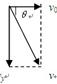
试题分析:(1)做出带电粒子的运动轨迹如图
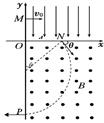
由三角形相关知识得
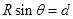
…(2分)
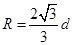
…………(1分)
(2)由
qvB=mv2/
R……(2分) 得
v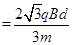
……(1分)
在
N点速度
v与
x轴正方向成
θ=60
°角射出电场,将速度分解如图
cos
θ= v0/
v……(1分)
得射出速度
v=2
v0,
v0=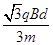
…(1分)
(3)粒子在电场中运动的时间
t1,有
d=
v0t1…(1分)
所以
t1=
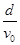
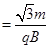
……(1分)
粒子在磁场中做匀速圆周运动的周期
T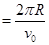
,故
T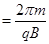
……(2分)
设粒子在磁场中运动的时间
t2,有
t2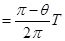
……(1分) 所以
t2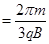 t
t=
t1+
t2,所以
t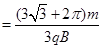
……(1分)
点评:不同场的分界面上,既是一种运动的结束,又是另一种运动的开始,寻找相关物理量尤其重要.
粒子在电场中运动偏转时,常用能量的观点来解决问题,有时也要运用运动的合成与分解.
点粒子做匀速圆周运动的圆心、半径及运动时间的确定也是本题的一个考查重点
圆心的确定:因洛伦兹力提供向心力,洛伦兹力总垂直于速度,画出带电粒子运动轨迹中任意两点(一般是射入磁场和射出磁场的两点)洛伦兹力的方向,其延长的交点即为圆心.或射入磁场和射出磁场的两点间弦的垂直平分线与一半径的交点即为圆心.
半径的确定:半径一般都在确定圆心的基础上用平面几何知识求解,常常是解直角三角形.运动时间的确定:利用圆心与弦切角的关系计算出粒子所转过的圆心角θ的大小,再者就是要正确画出粒子运动的轨迹图,能熟练的运用几何知识解决物理问题.

