试题分析：（1）当磁场B和电场E同时存在时，两种粒子都受力平衡，都满足
Eq=Bqv
所以两种粒子速度相同都为v=
①（2分）
当仅存在磁场时，带电粒子做匀速圆周运动，洛仑兹力充当向心力，两种粒子都满足
得
②（2分）
当磁场强度为B时，
P粒子的轨道半径r
1=l，Q粒子轨道半径为r
2=
③
由②可知当磁场为B
1减半时，两粒子做圆周运动的半径都加倍，此时 r
1′=2l，r
2′=
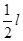
此时P粒子将打在M屏上，由几何关系可求出落点横坐标
所以P粒子亮点位置（
，l ） （1分）
而Q粒子仍打在N屏上，易得亮点位置（l，0） （1分）
（2）由上问①②③式，可得两粒子的荷质比及其与E、B的关系，对P、Q分别有
④
⑤（1分）
当仅存在电场时，P粒子将向右偏，y方向分运动为匀速直线运动
vt=l ⑥（1分）
x方向分运动为受电场力下的匀加速直线运动，有
⑦
⑧（1分）
结合④⑥⑦可得
⑨（1分）
由①④⑨可得
x
1=
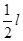
同理可以求得Q粒子在-x方向的偏转位移为
x
2=2l
故P、Q两粒子打在屏上的位置坐标分别为（
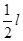
，l）、（-2l，l）。 （2分）
（3）由②和③可以得出结论，不论磁场为多少，P、Q两粒子的轨道半径R
1：R
2=4：1不变。因为两粒子速度大小相等，所以要想两粒子运动时间相等，即运动弧长相等，两粒子运动的圆弧圆心角之比必须为θ
1：θ
2=1：4。
如图粒子打在M屏上时，其运动轨迹圆弧圆心角θ（锐角）与半径R满足l=Rsinθ，不可能满足R
1：R
2=4：1和θ
1：θ
2=1：4。所以两粒子都打在M屏上不可能满足要求。 （2分）
两粒子都打在N屏上，圆心角都为π也不能满足要求。 （2分）
所以结果必然为P粒子打在M屏而Q粒子打在N屏，所以θ
2=π，而θ
1=
。
由几何关系易得此时R
1=
l，结合②③可求得此时
B
2=
，k=
（2分）
，请计算荧光屏上出现的所有亮点的位置坐标；