首页
>
考试
>
物理
>
高中物理
>
带电粒子在复合场中的运动
> 正文
返回
打印
如图所示，有一垂直于纸面向外的有界匀强磁场，磁场的磁感应强度为B，其边界为一等腰直角三角形（边界上有磁场），ACD为三角形的三个顶点，AC=AD=L．今有一质量为m、电荷量为+q
网友投稿 2023-04-12 00:00:00 互联网
◎ 题目
如图所示，有一垂直于纸面向外的有界匀强磁场，磁场的磁感应强度为B，其边界为一等腰直角三角形（边界上有磁场），ACD为三角形的三个顶点，AC=AD=L．今有一质量为m、电荷量为+q的粒子（不计重力），以速度v=
从CD边上的某点P既垂直于CD边又垂直于磁场的方向射入，然后从AD边上某点Q射出，则有（ ）
A．DP＜
L
B．DP＜
L
C．DQ≤
L
D．DQ≤
L
◎ 答案
◎ 解析
试题分析：粒子在磁场中做匀速圆周运动，洛伦兹力提供向心力，临界轨迹是恰好与AC边相切，然后结合几何关系分析即可．
解：A、B、粒子在磁场中做匀速圆周运动，洛伦兹力提供向心力，轨道半径为：
r=
=
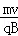
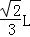
临界轨迹圆恰好与AC边相切，如图所示：
结合几何关系，有：
DP=CD﹣CP=CD﹣（CO﹣OP）=
﹣（
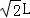
r﹣r）=
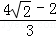
L
故DP小于
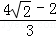
L，粒子可以从AD边射出；故A正确，B错误；
C、D、结合几何关系，根据勾股定理，有：
EO
2
+QE
2
=QO
2
即（r﹣AQ）
2
+QE
2
=r
2
（r﹣AQ）
2
+（L﹣r）
2
=r
2
解得：AQ=
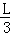
，故QD=
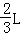
故粒子可以从AD边离D的
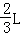
点射出，故C正确，D错误；
故选：AC．
点评：本题关键是先结合洛伦兹力提供向心力列式求解出轨道半径，然后画出临界轨迹，最后结合几何关系列式求解．
◎ 知识点
专家分析，试题“如图所示，有一垂直于纸面向外的有界匀强磁场，磁场的磁感应强度为B，其边界为一等腰直角三角形（边界上有磁场），ACD为三角形的三个顶点，AC=AD=L．今有一质量为m、电荷量为+q…”主要考查了你对 【带电粒子在复合场中的运动】 等知识点的理解和应用能力。关于这些知识点的“档案”，你可以点击相应的链接进行查看和学习。
http://www.00-edu.com/html/202304/444819.html
十二生肖
十二星座
从CD边上的某点P既垂直于CD边又垂直于磁场的方向射入，然后从AD边上某点Q射出，则有（ ）
L
L
L
L
=
﹣（
r﹣r）=
L
，故QD=
点射出，故C正确，D错误；