如图甲所示，足够长的光滑平行金属导轨MN、PQ所在平面与水平面成30°角，两导轨的间距l＝0.50m，一端接有阻值R＝1.0Ω的电阻．质量m＝0.10kg的金属棒ab置于导轨上，与导轨垂直，打印页面

如图甲所示，足够长的光滑平行金属导轨MN、PQ所在平面与水平面成30°角，两导轨的间距l＝0.50m，一端接有阻值R＝1.0Ω的电阻．质量m＝0.10kg的金属棒ab置于导轨上，与导轨垂直，

网友投稿 2023-04-20 00:00:00 互联网

◎ 题目

如图甲所示，足够长的光滑平行金属导轨MN、PQ所在平面与水平面成30°角，两导轨的间距l＝0.50 m，一端接有阻值R＝1.0 Ω的电阻．质量m＝0.10 kg的金属棒ab置于导轨上，与导轨垂直，电阻r＝0.25 Ω.整个装置处于磁感应强度B＝1. 0 T的匀强磁场中，磁场方向垂直于导轨平面向下．t＝0时刻，对金属棒施加一平行于导轨向上的外力F，使之由静止开始运动，运动过程中电路中的电流随时间t变化的关系如图乙所示．电路中其他部分电阻忽略不计，g取10 m/s².求：

(1)4.0 s末金属棒ab瞬时速度的大小；
(2)3.0 s末力F的瞬时功率；
(3)已知0～4.0 s时间内电阻R上产生的热量为0.64 J，试计算F对金属棒所做的功．

◎ 答案

(1)2. 0 m/s　(2)1.275 W　(3)3.0 J

◎ 解析

(1)由题图乙可得：t＝4.0 s时，I＝0.8 A.
根据I＝

，E＝Blv
解得：v＝2.0 m/s.
(2)由I＝

和感应电流与时间的线性关系可知，金属棒做初速度为零的匀加速直线运动．
由运动学规律v＝at
解得4.0 s内金属棒的加速度大小a＝0.5 m/s²
对金属棒进行受力分析，根据牛顿第二定律得：
F－mgsin 30°－F_安＝ma
又F_安＝BIl
由题图乙可得，t＝3.0 s时，I＝0.6 A
解得F_安＝0.3 N，外力F＝0.85 N
由速度与电流的关系可知t＝3.0 s时v＝1.5 m/s
根据P＝Fv，解得P＝1.275 W.
(3)根据焦耳定律：Q＝I²Rt　Q′＝I²rt
解得在该过程中金属棒上产生的热量Q′＝0.16 J
电路中产生的总热量为：Q_总＝0.80 J
根据能量守恒定律有：
W_F＝ΔE_p＋Q_总＋

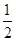
mv²
ΔE_p＝mgxsin 30°
x＝

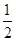
at²
解得ΔE_p＝2.0 J
F对金属棒所做的功W_F＝3.0 J.

◎ 知识点

专家分析，试题“如图甲所示，足够长的光滑平行金属导轨MN、PQ所在平面与水平面成30°角，两导轨的间距l＝0.50m，一端接有阻值R＝1.0Ω的电阻．质量m＝0.10kg的金属棒ab置于导轨上，与导轨垂直，…”主要考查了你对【电磁感应现象的综合应用】等知识点的理解和应用能力。关于这些知识点的“档案”，你可以点击相应的链接进行查看和学习。

http://www.00-edu.com/html/202304/455828.html十二生肖
十二星座