如图，在矩形ABCD中，AB=8cm，AD=6cm，点F是CD延长线上一点，且DF=2cm。点P、Q分别从A、C同时出发，以1cm/s的速度分别沿边AB、CB向终点B运动，当一点运动到终点B时，另一点也-九年级数学打印页面

如图，在矩形ABCD中，AB=8cm，AD=6cm，点F是CD延长线上一点，且DF=2cm。点P、Q分别从A、C同时出发，以1cm/s的速度分别沿边AB、CB向终点B运动，当一点运动到终点B时，另一点也-九年级数学

[db:作者] 2019-02-24 00:00:00 零零社区

题文

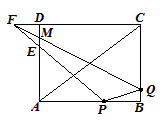
如图，在矩形ABCD中，AB=8cm，AD=6cm，点F是CD延长线上一点，且DF=2cm。点P、Q分别从A、C同时出发，以1cm/s的速度分别沿边AB、CB向终点B运动，当一点运动到终点B时，另一点也停止运动。FP、FQ分别交AD于E、M两点，连结PQ、AC，设运动时间为t （s）。

（1）用含有t的代数式表示DM的长；
（2）设△FCQ的面积为y （cm²），求y与t之间的函数关系式；
（3）线段FQ能否经过线段AC的中点，若能，请求出此时t的值，若不能，请说明理由；
（4）设△FPQ的面积为S （cm²），求S与t之间的函数关系式，并回答，在t的取值范围内，S是如何随t的变化而变化的。
题型：解答题难度：偏难

答案

解: （1）
（2） S_△FCQ=5t　
（3）
（4）

S随t的增大而减小。
即：从t=0，S=30变化到 t=6，S=6

据专家权威分析，试题“如图，在矩形ABCD中，AB=8cm，AD=6cm，点F是CD延长线上一点，且D..”主要考查你对写代数式，正比例函数的定义，求二次函数的解析式及二次函数的应用，直线，线段，射线，正方形，正方形的性质，正方形的判定等考点的理解。关于这些考点的“档案”如下：

写代数式正比例函数的定义求二次函数的解析式及二次函数的应用直线，线段，射线正方形，正方形的性质，正方形的判定

考点名称：写代数式

代数式：
由数和表示数的字母经有限次加、减、乘、除、乘方和开方等代数运算所得的式子，或含有字母的数学表达式称为代数式。
数的一切运算规律也适用于代数式。单独的一个数或者一个字母也是代数式。
例如：ax+2b，－2/3，b^2/26，√a+√2等。
带有“(≥)” “=”“≠”等符号的不是代数式
注意：
1、不包括等于号（=、≡）、不等号（≠、≤、≥、<、>、≮、≯）、约等号≈。
2、可以有绝对值。例如：|x|，|-2.25| 等。
代数式的书写要求：
一、数字与数字相乘时，中间的乘号不能用“? ”代替，更不能省略不写。
如：4乘5，写作4×5，不能写成4?5，更不能写成45
二、数字与字母相乘时，中间的乘号可以省略不写，并且数字放在字母的前面。
如： a的5倍，写作：5a 不要写成a5。
三、两个字母相乘时，中间的乘号可以省略不写，字母无顺序性
如： a乘b ，写成ab或ba
四、当字母和带分数相乘时，要把带分数化成假分数。
如：3 1/2 乘a 写作：7/2 a 不要写成32/1a
五、含有字母的除法运算中，最后结果要写成分数形式，分数线相当于除号。
如：5除以a 写作5/a ，不要写成5÷a ； c除以 d写作，不要写成 c÷ d
六、如果代数式后面带有单位名称，是乘除运算结果的直接将单位名称写在代数式后面，若代数式是带加减运算且须注明单位的，要把代数式括起来，后面注明单位。
如：甲同学买了5本书，乙同学买了a 本书，他们一共买了（5+a ）本。
代数式的书写格式：
（1）数与字母，字母与字母相乘，乘号可以省略，也可写成“.”；
（2）数字要写在前面；
（3）带分数一定要写成假分数；
（4）在含有字母的除法中，一般不用“÷”号，而写成分数的形式；
（5）式子后面有单位时，和差形式的代数式要在单位前把代数式括起来。
代数式：

考点名称：正比例函数的定义

正比例函数定义：
一般地，形如y=kx（k是常数，k≠0）的函数，叫做正比例函数，其中k叫做比例系数。
正比例函数属于一次函数，但一次函数却不一定是正比例函数。
正比例函数是一次函数的特殊形式，即一次函数y=kx+b中，若b=0，即所谓“y轴上的截距”为零，则为正比例函数。
正比例函数的关系式表示为：y=kx（k为比例系数）
当k>0时（一三象限），k越大，图像与y轴的距离越近。函数值y随着自变量x的增大而增大。
当k<0时（二四象限），k越小，图像与y轴的距离越近。自变量x的值增大时，y的值则逐渐减小。
正比例函数性质：
定义域
R（实数集）

值域
R（实数集）

奇偶性
奇函数

单调性
当k>0时，图像位于第一、三象限，从左往右，y随x的增大而增大（单调递增），为增函数；
当k<0时，图像位于第二、四象限，从左往右，y随x的增大而减小（单调递减），为减函数。

周期性
不是周期函数。

对称性
对称点：关于原点成中心对称
对称轴：自身所在直线；自身所在直线的垂直平分线

考点名称：求二次函数的解析式及二次函数的应用

求二次函数的解析式：
最常用的方法是待定系数法，根据题目的特点，选择恰当的形式，一般，有如下几种情况：
（1）已知抛物线上三点的坐标，一般选用一般式；
（2）已知抛物线顶点或对称轴或最大（小）值，一般选用顶点式；
（3）已知抛物线与x轴的两个交点的横坐标，一般选用两点式；
（4）已知抛物线上纵坐标相同的两点，常选用顶点式。

二次函数的应用：
（1）应用二次函数才解决实际问题的一般思路：
理解题意；
建立数学模型；
解决题目提出的问题。
（2）应用二次函数求实际问题中的最值：
即解二次函数最值应用题，设法把关于最值的实际问题转化为二次函数的最值问题，然后按求二次函数最值的方法求解。
求最值时，要注意求得答案要符合实际问题。
二次函数的三种表达形式：
①一般式：
y=ax2+bx+c(a≠0,a、b、c为常数)，顶点坐标为 [,]
把三个点代入函数解析式得出一个三元一次方程组，就能解出a、b、c的值。

②顶点式：
y=a(x-h)2+k(a≠0,a、h、k为常数),顶点坐标为对称轴为直线x=h，顶点的位置特征和图像的开口方向与函数y=ax²的图像相同，当x=h时，y最值=k。
有时题目会指出让你用配方法把一般式化成顶点式。
例：已知二次函数y的顶点(1,2)和另一任意点(3,10)，求y的解析式。
解：设y=a(x-1)2+2，把(3,10)代入上式，解得y=2(x-1)2+2。
注意：与点在平面直角坐标系中的平移不同，二次函数平移后的顶点式中，h>0时，h越大，图像的对称轴离y轴越远，且在x轴正方向上，不能因h前是负号就简单地认为是向左平移。
具体可分为下面几种情况：
当h>0时，y=a(x-h)2的图象可由抛物线y=ax2向右平行移动h个单位得到；
当h<0时，y=a(x-h)2的图象可由抛物线y=ax2向左平行移动|h|个单位得到；
当h>0,k>0时，将抛物线y=ax2向右平行移动h个单位，再向上移动k个单位，就可以得到y=a(x-h)2+k的图象；
当h>0,k<0时，将抛物线y=ax2向右平行移动h个单位，再向下移动|k|个单位可得到y=a(x-h)2+k的图象；
当h<0,k>0时，将抛物线y=ax2向左平行移动|h|个单位，再向上移动k个单位可得到y=a(x-h)2+k的图象；
当h<0,k<0时，将抛物线y=ax2向左平行移动|h|个单位，再向下移动|k|个单位可得到y=a(x-h)2+k的图象。

③交点式：
y=a(x-x₁)(x-x₂) (a≠0) [仅限于与x轴即y=0有交点时的抛物线，即b²-4ac≥0] .
已知抛物线与x轴即y=0有交点A（x₁，0）和 B（x₂，0）,我们可设y=a(x-x₁)(x-x₂),然后把第三点代入x、y中便可求出a。

由一般式变为交点式的步骤：
二次函数
∵x₁+x₂=-b/a， x₁?x₂=c/a(由韦达定理得),
∴y=ax2+bx+c
=a(x2+b/ax+c/a)
=a[x2-(x₁+x₂)x+x₁?x₂]
=a(x-x₁)(x-x₂).
重要概念：
a，b，c为常数，a≠0，且a决定函数的开口方向。a>0时，开口方向向上；
a<0时，开口方向向下。a的绝对值可以决定开口大小。
a的绝对值越大开口就越小，a的绝对值越小开口就越大。
能灵活运用这三种方式求二次函数的解析式；
能熟练地运用二次函数在几何领域中的应用；
能熟练地运用二次函数解决实际问题。
二次函数的其他表达形式：
①牛顿插值公式:
f(x)=f[x₀]+f[x₀,x₁](x-x₀)+f[x₀,x₁,x₂](x-x₀)(x-x₁)+...f[x₀,...x_n](x-x₀)...(x-_xn-1)+Rn(x)由此可引导出交点式的系数a=y/(x·x)(y为截距)　
二次函数表达式的右边通常为二次三项式。

双根式
y=a(x-x₁)*(x-x2)
若ax2+bx+c=0有两个实根x₁,x₂，则y=a(x-x₁)(x-x₂)此抛物线的对称轴为直线x=(x₁+x₂)/2。

③三点式
已知二次函数上三个点，（x₁,f(x₁)）（x₂,f(x₂)）（x₃,f(x₃)）
则f(x)=f(x₃)(x-x₁)(x-x₂)/(x₃-x₁)(x₃-x₂)+f(x₂)(x-x₁)*(x-x₃)/(x₂-x₁)(x₂-x₃)+f(x₁)(x-x₂)(x-x₃)/(x₁-x₂)(x₁-x₃)
与X轴交点的情况
当△=b2-4ac>0时，函数图像与x轴有两个交点。(x₁,0), (x₂,0);
当△=b2-4ac=0时，函数图像与x轴只有一个交点。(-b/2a，0)。
Δ=b2-4ac<0时，抛物线与x轴没有交点。
X的取值是虚数（x=-b±√b2－4ac的值的相反数，乘上虚数i，整个式子除以2a）
二次函数解释式的求法：
就一般式y=ax2＋bx＋c（其中a，b，c为常数，且a≠0）而言，其中含有三个待定的系数a ，b ，c．求二次函数的一般式时，必须要有三个独立的定量条件，来建立关于a ，b ，c 的方程，联立求解，再把求出的a ，b ，c 的值反代回原函数解析式，即可得到所求的二次函数解析式。

1.巧取交点式法：
知识归纳：二次函数交点式：y＝a(x－x₁)(x－x₂) （a≠0）x₁，x₂分别是抛物线与x轴两个交点的横坐标。
已知抛物线与x轴两个交点的横坐标求二次函数解析式时，用交点式比较简便。
①典型例题一：告诉抛物线与x轴的两个交点的横坐标，和第三个点，可求出函数的交点式。
例：已知抛物线与x轴交点的横坐标为-2和1 ，且通过点（2，8），求二次函数的解析式。
点拨：
解设函数的解析式为y＝a(x+2)(x-1)，
∵过点（2，8），
∴8＝a(2+2)(2-1)。
解得a=2，
∴抛物线的解析式为：
y＝2(x+2)(x-1)，
即y＝2x2+2x-4。

②典型例题二：告诉抛物线与x轴的两个交点之间的距离和对称轴，可利用抛物线的对称性求解。
例：已知二次函数的顶点坐标为（3，-2），并且图象与x轴两交点间的距离为4，求二次函数的解析式。
点拨：
在已知抛物线与x轴两交点的距离和顶点坐标的情况下，问题比较容易解决．由顶点坐标为（3，-2）的条件，易知其对称轴为x＝3，再利用抛物线的对称性，可知图象与x轴两交点的坐标分别为（1，0）和（5，0）。此时，可使用二次函数的交点式，得出函数解析式。

2.巧用顶点式：
顶点式y=a(x－h)²+k（a≠0），其中（h，k）是抛物线的顶点。当已知抛物线顶点坐标或对称轴，或能够先求出抛物线顶点时，设顶点式解题十分简洁，因为其中只有一个未知数a。在此类问题中，常和对称轴，最大值或最小值结合起来命题。在应用题中，涉及到桥拱、隧道、弹道曲线、投篮等问题时，一般用顶点式方便．
①典型例题一：告诉顶点坐标和另一个点的坐标，直接可以解出函数顶点式。
例：已知抛物线的顶点坐标为（-1，-2），且通过点（1，10），求此二次函数的解析式。
点拨：
解∵顶点坐标为（-1，-2），
故设二次函数解析式为y=a(x+1)²-2 （a≠0）。
把点（1，10）代入上式，得10=a·(1+1)²-2。
∴a=3。
∴二次函数的解析式为y=3(x+1)²-2，即y=3x²+6x+1。

②典型例题二：
如果a>0，那么当时，y有最小值且y_最小=；
如果a<0，那么，当时，y有最大值，且y_最大=。
告诉最大值或最小值，实际上也是告诉了顶点坐标，同样也可以求出顶点式。
例：已知二次函数当x＝4时有最小值－3，且它的图象与x轴两交点间的距离为6，求这个二次函数的解析式。
点拨：
析解∵二次函数当x＝4时有最小值－3，∴顶点坐标为（4，-3），对称轴为直线x＝4，抛物线开口向上。
由于图象与x轴两交点间的距离为6，根据图象的对称性就可以得到图象与x轴两交点的坐标是（1，0）和（7，0）。
∴抛物线的顶点为（4，-3）且过点（1，0）。
故可设函数解析式为y＝a(x－4)²－3。
将（1，0）代入得0＝a(1－4)²－3, 解得a＝13．
∴y＝13(x－4)²-3，即y＝13x²－83x＋73。
③典型例题三：告诉对称轴，相当于告诉了顶点的横坐标，综合其他条件，也可解出。
例如：
（1）已知二次函数的图象经过点A（3，-2）和B（1，0），且对称轴是直线x＝3．求这个二次函数的解析式.
（2）已知关于x的二次函数图象的对称轴是直线x=1，图象交y轴于点（0，2），且过点（-1，0），求这个二次函数的解析式.
（3）已知抛物线的对称轴为直线x=2，且通过点（1，4）和点（5，0），求此抛物线的解析式.
（4）二次函数的图象的对称轴x=-4，且过原点，它的顶点到x轴的距离为4，求此函数的解析式．

④典型例题四：利用函数的顶点式，解图像的平移等问题非常方便。
例：把抛物线y=ax2+bx+c的图像向右平移3 个单位, 再向下平移2 个单位, 所得图像的解析式是y=x2-3x+5, 则函数的解析式为_______。
点拨：
解先将y=x2-3x+5化为y=(x-32)2+5-94, 即y=(x-32)2+114。
∵它是由抛物线的图像向右平移3 个单位, 再向下平移2 个单位得到的，
∴原抛物线的解析式是y=(x-32+3)2+114+2=(x+32)2+194=x2+3x+7。

考点名称：直线，线段，射线

基本概念：
直线：一根拉得很紧的线，就给我们以直线的形象，直线是直的，并且是向两方无限延伸的。一条直线可以用一个小写字母表示。
线段：直线上两个点和它们之间的部分叫做线段，这两个点叫做线段的端点。一条线段可用它的端点的两个大写字母来表示。
射线：直线上一点和它一旁的部分叫做射线。这个点叫做射线的端点。一条射线可以用端点和射线上另一点来表示。
注意：
①线和射线无长度，线段有长度。
②直线无端点，射线有一个端点，线段有两个端点。

直线、射线、线段的基本性质：

图形表示法端点延长线能否度量基本性质

直线没有端点的一条线一条线,
不要端点无可以向两边无限延长否两端都没有端点,可以无限延长,不可测量的线

射线只有一个端点的一条线一条线,
只有一边有端点
一个可以向一边无限延长否一端有端点,可以向一边无限延长,不可测量的线

线段两边都有端点的一条线一条线,两边都有端点两个不能延长能两端都有端点,不能延长,可测量的线

直线、射线、线段区别：
直线没有端点,2边可无限延长；
射线有1端有端点，另一端可无限延长；
线段,有2个端点,而2个端点间的距离就是这条线段的长度。

直线除了“直”这个特点外，还有一个很重要的特点，那就是它可以向两个方向无限延伸，永远没有尽头，所以，直线是不可能度量的。因此，在画直线时，要画出没有端点的直线，表示可以无限延伸；
射线只有一个端点，可以向一个方向无限延伸，也永远没有尽头。所以，射线也是不可能度量的。直线上任意的一点可以把这条直线分成两条方向相反的射线，因此，射线是直线的一部分。虽然射线是直线的一部分，但由于它们都是不能度量的，所以，它们之间没有长短可以比较；
线段有两个端点，它有一定的长度，可以度量。线段也是直线的一部分。
各种图形表示方法：
直线：一个小写字母或两个大写字母，但前面必须加“直线”两字，如：直线l，直线m；直线AB，直线CD。
例：直线l；直线AB。
射线：一个小写字母或端点的大写字母。和射线上的一个大写字母，前面必须加“射线”两字。如：射线a；射线OA。
例：射线AB。
线段：用表示端点的大写字母表示，如线段AB；用一个小写字母表示，如线段a。
例：线段AB；线段a 。

考点名称：正方形，正方形的性质，正方形的判定

正方形的定义：
有一组邻边相等并且有一个角是直角的平行四边形叫做正方形。
特殊的长方形。
四条边都相等且四个角都是直角的四边形叫做正方形。
有一组邻边相等的矩形是正方形。
有一个角为直角的菱形是正方形。
对角线平分且相等，并且对角线互相垂直的四边形为正方形。
对角线相等的菱形是正方形。
正方形的性质：
1、边：两组对边分别平行；四条边都相等；相邻边互相垂直
2、内角：四个角都是90°；
3、对角线：对角线互相垂直；对角线相等且互相平分；每条对角线平分一组对角；
4、对称性：既是中心对称图形，又是轴对称图形（有四条对称轴）；
5、正方形具有平行四边形、菱形、矩形的一切性质；
6、特殊性质：正方形的一条对角线把正方形分成两个全等的等腰直角三角形，对角线与边的夹角是45°；
正方形的两条对角线把正方形分成四个全等的等腰直角三角形；
7、在正方形里面画一个最大的圆，该圆的面积约是正方形面积的78.5%；
正方形外接圆面积大约是正方形面积的157%。
8、正方形是特殊的长方形。
正方形的判定：
判定一个四边形为正方形的一般顺序如下：先证明它是平行四边形，再证明它是菱形（或矩形），最后证明它是矩形（或菱形）。
1：对角线相等的菱形是正方形。
2：有一个角为直角的菱形是正方形。
3：对角线互相垂直的矩形是正方形。
4：一组邻边相等的矩形是正方形。
5：一组邻边相等且有一个角是直角的平行四边形是正方形。
6：对角线互相垂直且相等的平行四边形是正方形。
7：对角线相等且互相垂直平分的四边形是正方形。
8：一组邻边相等，有三个角是直角的四边形是正方形。
9：既是菱形又是矩形的四边形是正方形。

有关计算公式：
若S为正方形的面积，C为正方形的周长，a为正方形的边长，则
正方形面积计算公式：S =a×a（即a的2次方或a的平方），或S=对角线×对角线÷2；
正方形周长计算公式: C=4a 。
S_正方形=。（正方形边长为a，对角线长为b）

http://www.00-edu.com/ks/shuxue/2/24/2019-02-24/683766.html十二生肖
十二星座