|
题文
设a,B是常数,不等式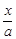 + +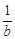 >0的解集为x< >0的解集为x<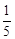 ,则关于x的不等式bx-a>0的解集是( )。 ,则关于x的不等式bx-a>0的解集是( )。 |
题型:单选题 难度:中档
答案
分析:这是一个含有字母系数的不等式,仔细观察 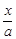 + +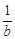 >0,通过移项、系数化为1求得解集,由不等式解集是x< >0,通过移项、系数化为1求得解集,由不等式解集是x<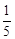 ,不等号的方向已改变,说明运用的是不等式的性质3,运用性质3的前提是两边都乘以(或除以)同一个负数,从而求出a<0,b>0.再通过移项、系数化为1求得关于x的不等式bx-a>0解集. ,不等号的方向已改变,说明运用的是不等式的性质3,运用性质3的前提是两边都乘以(或除以)同一个负数,从而求出a<0,b>0.再通过移项、系数化为1求得关于x的不等式bx-a>0解集.
解答:解:不等式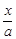 + +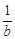 >0的解集为 >0的解集为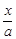 >- >-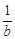 , ,
x<-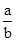 ,x< ,x<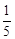 . .
所以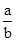 =- =-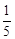 且a<0,b>0, 且a<0,b>0,
所以不等式bx-a>0的解集为
bx>a
x>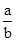
x>-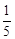 . .
故选C. |
据专家权威分析,试题“设a,B是常数,不等式+>0的解集为x<,则关于x的不等式bx..”主要考查你对 不等式的性质,不等式的定义,一元一次不等式的解法,一元一次不等式组的定义 等考点的理解。关于这些考点的“档案”如下:
不等式的性质不等式的定义一元一次不等式的解法一元一次不等式组的定义
考点名称:不等式的性质 考点名称:不等式的定义 考点名称:一元一次不等式的解法 考点名称:一元一次不等式组的定义
|

