|
题文
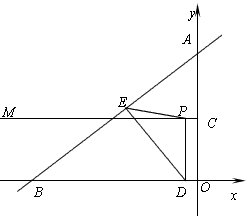
如图,直线y=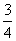 x+3和x轴、y轴的交点分别为点B、A,点C是OA的中点,过点C向左方作射线CM⊥y轴,点D是线段OB上一动点,不和点B重合,DP⊥CM于点P,DE⊥AB于点E,连接PE x+3和x轴、y轴的交点分别为点B、A,点C是OA的中点,过点C向左方作射线CM⊥y轴,点D是线段OB上一动点,不和点B重合,DP⊥CM于点P,DE⊥AB于点E,连接PE
(1)求A、B、C三点的坐标;
(2)设点D的横坐标为x,△BED的面积为S,求S关于x的函数关系式;
(3)是否存在点D,使△DPE为等腰三角形?若存在,请直接写出所有满足要求的x的值;若不存在,说明理由. |
|
|
题型:解答题 难度:偏难
答案
解:(1)将x=0代入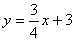 ,得y=3,故点A的坐标为(0,3) ,得y=3,故点A的坐标为(0,3)
∵C为OA的中点,则C点坐标为(0,1.5);
将y=0代入 ,得x=-4,故点B的坐标为(-4,0) ,得x=-4,故点B的坐标为(-4,0)
则A、B、C三点的坐标分别为(0,3),(-4,0),(0,1.5)
(2)由(1)得OB=4,OA=3,则由勾股定理可得,AB=5
∵点P的横坐标为x,故OD= -x,则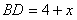
又由已知得,∠DEB=∠AOB=90°
∴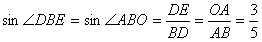 , , , ,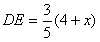
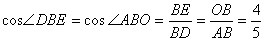 , ,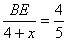 , ,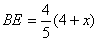
∴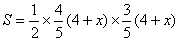 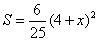 ( ( ) )
(3)符合要求的点有三个,x=0,-1.5,-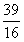 |
据专家权威分析,试题“如图,直线y=x+3和x轴、y轴的交点分别为点B、A,点C是OA的中点,..”主要考查你对 一次函数的图像,求二次函数的解析式及二次函数的应用,等腰三角形的性质,等腰三角形的判定,勾股定理 等考点的理解。关于这些考点的“档案”如下:
一次函数的图像求二次函数的解析式及二次函数的应用等腰三角形的性质,等腰三角形的判定勾股定理
考点名称:一次函数的图像 考点名称:求二次函数的解析式及二次函数的应用 考点名称:等腰三角形的性质,等腰三角形的判定 考点名称:勾股定理
|

