零零教育信息网 首页 > 考试 > 数学 > 初中数学 > 一次函数与一元一次不等式（一元一次方程） > 正文 返回　打印

我们知道，在数轴上，x=1表示一个点，而在平面直角坐标系中，x=1表示一条直线；我们还知道，以二元一次方程2x-y+1=0的所有解为坐标的点组成的图形就是一次函数y=2x+1的图象，-数学
[db:作者]  2019-03-25 00:00:00  零零社区

题文

我们知道，在数轴上，x=1表示一个点，而在平面直角坐标系中，x=1表示一条直线；我们还知道，以二元一次方程2x-y+1=0的所有解为坐标的点组成的图形就是一次函数y=2x+1的图象，它也是一条直线，如图1．
观察图1可以得出：直线x=1与直线y=2x+1的交点P的坐标（1，3）就是
方程组

x=1
2x-y+1=0
的解，所以这个方程组的解为

x=1
y=3
．
在直角坐标系中，x≤1表示一个平面区域，即直线x=1以及它左侧的部分，如图②；y≤2x+1也表示一个平面区域，即直线y=2x+1以及它下方的部分，如图3；
那么，

x≤1
y≤2x+1
y＞0
所围成的区域就是图4中的阴影部分．

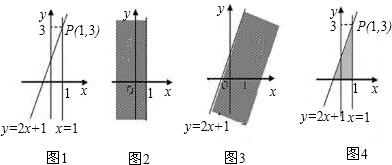
回答下列问题：
（1）在下面的直角坐标系中，用作图象的方法求出方程组

x=2
y=-
3
2
x+3
的解；
（2）在右面的直角坐标系中用阴影表示，

x≤2
y≤-x2+2x+3
y≥-
3
2
x+3
所围成的区域．
题型：解答题  难度：中档

答案

（1）在坐标系中分别作出直线x=2和直线y=-
3
2
x+3，
这两条直线的交点是（2，0）．
则x=2，y=0就是方程组

x=2
y=-
3
2
x+3
的解．

（2）在（1）问的前提下作出y=-x2+2x+3的图象，
则

x≤2
y≤-x2+2x+3
y≥-
3
2
x+3
所围成的区域如图阴影所示．

据专家权威分析，试题“我们知道，在数轴上，x=1表示一个点，而在平面直角坐标系中，x=1..”主要考查你对  一次函数与一元一次不等式（一元一次方程）  等考点的理解。关于这些考点的“档案”如下：

一次函数与一元一次不等式（一元一次方程）

考点名称：一次函数与一元一次不等式（一元一次方程）

  • 一次函数和方程关系:
    一次函数 一元一次方程
    形式 y=kx+b ax+b=0
    内容 表示的是一对(x，y)之间的关系，
    它有无数对解    		 表示的是未知数x的值，
    最多只有1个值
    相互关系 一次函数与x轴交点的横坐标就是相应的一元一次方程的根
    例如：
    y=4x+8与x轴的交点是(-2，0),
    则一元一次方程4x+8=0的根是x=-2。

    函数和不等式:
    解不等式的方法：从函数的角度看，就是寻求使一次函数y=kx+b的值大于（或小于）0的自变量x的取值范围；
    从函数图像的角度看，就是确定直线y=kx+b在x轴上（或下）方部分所有的点的横坐标所构成的集合。
    对应一次函数y=kx+b，它与x轴交点为（-b/k，0）。
    当k>0时，不等式kx+b>0的解为：x>- b/k，不等式kx+b<0的解为：x<- b/k；
    当k<0的解为：不等式kx+b>0的解为：x<- b/k，不等式kx+b<0的解为：x>- b/k。

  • 一元一次不等式与一元一次方程、一次函数的关系：
    1.一元一次不等式ax+b>0（a≠0）是一次函数y=ax+b（a≠0）的函数值>0的情形；
    一元一次不等式ax+b<0（a≠0）是一次函数y=ax+b（a≠0）的函数值<0的情形。
    2.直线y=ax+b上使函数值y>0（x轴上方的图像）的x的取值范围是ax+b>0的解集；
    使函数值y<0（x轴下方的图像）的x的取值范围是ax+b<0的解集。
    3.一元一次方程ax+b=0（a≠0）是一次函数y=ax+b（a≠0）的函数值=0的情形；
    反之，使函数值y=0的x的取值就是方程ax+b=0（a≠0）的解。
http://www.00-edu.com/ks/shuxue/2/68/2019-03-25/896495.html十二生肖
十二星座