|
题文
如图,点A,B分别在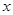 轴, 轴, 轴上,点D在第一象限内,DC⊥ 轴上,点D在第一象限内,DC⊥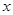 轴于点C,AO=CD=2,AB=DA= 轴于点C,AO=CD=2,AB=DA= ,反比例函数 ,反比例函数 的图象过CD的中点E。 的图象过CD的中点E。

(1)求证:△AOB≌△DCA;
(2)求 的值; 的值;
(3)△BFG和△DCA关于某点成中心对称,其中点F在 轴上,试判断点G是否在反比例函数的图象上,并说明理由。( 轴上,试判断点G是否在反比例函数的图象上,并说明理由。( |
题型:解答题 难度:中档
答案
(1)证明见解析
(2)K=3
(3)点G在反比例函数图象上 |
试题分析:(1)利用HL可证△AOB≌△DCA
由勾股定理可求出AC的长,从而得到OC的长,可得E坐标,代入即得
(3)由△BFG和△DCA关于某点成中心对称可知BF=DC=2,FG=AC=1,从而可得点G坐标,代入判断即可
试题解析:(1)∵点A,B分别在X,Y轴上,DC⊥X轴于点C
∴∠AOB=∠DCA=90°
∵AO=CD=2,AB=DA=
∴△AOB≌△DCA
(2)∵∠DCA=90°,DA= ,CD=2 ,CD=2
∴AC=
∴OC=OA+AC=2+1=3
∵E是CD的中点
∴E(3,1)
∵反比例函数 的图象过点E 的图象过点E
∴K=3
(3)∵△BFG和△DCA关于某点成中心对称
∴BF=DC=2,FG=AC=1
∵点F在Y轴上
∴OF=OB+BF=1+2=3
∴G(1,3)
把X=1代入 中得Y=3 中得Y=3
∴点G在反比例函数图象上 |
据专家权威分析,试题“如图,点A,B分别在轴,轴上,点D在第一象限内,DC⊥轴于点C,AO=..”主要考查你对 反比例函数的定义,反比例函数的图像,反比例函数的性质,求反比例函数的解析式及反比例函数的应用 等考点的理解。关于这些考点的“档案”如下:
反比例函数的定义反比例函数的图像反比例函数的性质求反比例函数的解析式及反比例函数的应用
考点名称:反比例函数的定义 考点名称:反比例函数的图像 考点名称:反比例函数的性质 考点名称:求反比例函数的解析式及反比例函数的应用
|

