如图，过点O作直线与双曲线y=（k≠0）交于A、B两点，过点B作BC⊥x轴于点C，作BD⊥y轴于点D．在x轴上分别取点E、F，使点A、E、F在同一条直线上，且AE=AF．设图中矩形ODBC的面积为S1，-八年级数学打印页面

如图，过点O作直线与双曲线y=（k≠0）交于A、B两点，过点B作BC⊥x轴于点C，作BD⊥y轴于点D．在x轴上分别取点E、F，使点A、E、F在同一条直线上，且AE=AF．设图中矩形ODBC的面积为S1，-八年级数学

[db:作者] 2019-04-10 00:00:00 互联网

题文

如图，过点O作直线与双曲线y=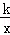（k≠0）交于A、B两点，过点B作BC⊥x轴于点C，作BD⊥y轴于点D．在x轴上分别取点E、F，使点A、E、F在同一条直线上，且AE=AF．设图中矩形ODBC的面积为S₁，△EOF的面积为S₂，则S₁、S₂的数量关系是（　　）

A．S₁=S₂ B．2S₁=S₂ C．3S₁=S₂ D．4S₁=S₂
题型：单选题难度：中档

答案

B

试题分析：设A点坐标为（m，n），
过点O的直线与双曲线y=交于A、B两点，则A、B两点关与原点对称，则B的坐标为（﹣m，﹣n）；
矩形OCBD中，易得OD=﹣n，OC=m；则S₁=﹣mn；
在Rt△EOF中，AE=AF，故A为EF中点，
由中位线的性质可得OF=﹣2n，OE=2m；
则S₂=OF×OE=﹣2mn；
故2S₁=S₂．
故选B．

据专家权威分析，试题“如图，过点O作直线与双曲线y=（k≠0）交于A、B两点，过点B作BC⊥x轴于..”主要考查你对反比例函数的定义，反比例函数的图像，反比例函数的性质，求反比例函数的解析式及反比例函数的应用等考点的理解。关于这些考点的“档案”如下：

反比例函数的定义反比例函数的图像反比例函数的性质求反比例函数的解析式及反比例函数的应用

考点名称：反比例函数的定义

一般地，函数（k是常数，k≠0）叫做反比例函数，自变量x的取值范围是x≠0的一切实数，函数值的取值范围也是一切非零实数。
注：
（1）因为分母不能为零，所以反比例函数函数的自变量x不能为零，同样y也不能为零；
（2）由，所以反比例函数可以写成的形式，自变量x的次数为-1；
（3）在反比例函数中，两个变量成反比例关系，即，因此判定两个变量是否成反比例关系，应看是否能写成反比例函数的形式，即两个变量的积是不是一个常数。

表达式：
x是自变量，y是因变量，y是x的函数
自变量的取值范围：
①在一般的情况下,自变量x的取值范围可以是不等于0的任意实数；
②函数y的取值范围也是任意非零实数。

反比例函数性质：
①反比例函数的表达式中，等号左边是函数值y，等号右边是关于自变量x的分式，分子是不为零的常数k，分母不能是多项式，只能是x的一次单项式；
②反比例函数表达式中，常数（也叫比例系数）k≠0是反比例函数定义的一个重要组成部分;
③反比例函数（k是常数，k≠0）的自变量x的取值范围是不等式0的任意实数，函数值y的取值范围也是非零实数。

考点名称：反比例函数的图像

反比例函数的图象：
反比例函数的图像是双曲线，它有两个分支，这两个分支分别位于第一、三象限，或第二、四象限，它们关于原点对称。由于反比例函数中自变量x≠0，函数y≠0，所以，它的图像与x轴、y轴都没有交点，即双曲线的两个分支无限接近坐标轴，但永远达不到坐标轴。
反比例函数的图像属于以原点为对称中心的中心对称的双曲线，反比例函数图像中每一象限的每一支曲线会无限接近X轴Y轴但不会与坐标轴相交（y≠0）。
反比例函数图象的画法：
（1）列表：

（2）描点：在平面直角坐标系中标出点。
（3）连线：用平滑的曲线连接点。
当双曲线在一三象限，K>0，在每个象限内，Y随X的增大而减小。
当双曲线在二四象限，K<0，在每个象限内，Y随X的增大而增大。
常见画法当两个数相等时那么曲线呈弯月型。
k的意义及应用：
过反比例函数（k≠0），图像上一点P（x,y），作两坐标轴的垂线，两垂足、原点、P点组成一个矩形，矩形的面积。过反比例函数过一点，作垂线，三角形的面积为。
研究函数问题要透视函数的本质特征。反比例函数中，比例系数k有一个很重要的几何意义，那就是：过反比例函数图象上任一点P作x轴、y轴的垂线PM、PN，垂足为M、N则矩形PMON的面积
所以，对双曲线上任意一点作x轴、y轴的垂线，它们与x轴、y轴所围成的矩形面积为常数。从而有k的绝对值。在解有关反比例函数的问题时，若能灵活运用反比例函数中k的几何意义，会给解题带来很多方便。

推论内容：一次函数y=x+b或y=-x+b若与反比例函数存在两个交点，若设2点的横坐标分别为x₁,x₂，那么这两个交点与原点连线和两点之间的连线所构成的三角形面积为
不同象限分比例函数图像：

常见画法：

考点名称：反比例函数的性质

反比例函数性质：
1.当k>0时，图象分别位于第一、三象限；
当k<0时，图象分别位于第二、四象限。
2.当k>0,在同一个象限内，y随x的增大而减小；
当k<0时，在同一个象限，y随x的增大而增大。
3.当k>0时，函数在x<0上为减函数、在x>0上同为减函数；
当k<0时，函数在x<0上为增函数、在x>0上同为增函数。
定义域为x≠0；值域为y≠0。
4.因为在y=k/x(k≠0)中，x不能为0，y也不能为0，所以反比例函数的图象不可能与x轴相交，也不可能与y轴相交.
5. 在一个反比例函数图象上任取两点P，Q，过点P，Q分别作x轴，y轴的平行线，与坐标轴围成的矩形面积为S1，S2则S1＝S2 ,且等于|k|.
6. 反比例函数的图象既是轴对称图形，又是中心对称图形，它有两条对称轴 y=x ，y=-x，对称中心是坐标原点.
函数图象位置和函数值的增减：
反比例函数:，反比例函数的性质主要研究它的图象的位置和函数值的增减情况，列表归纳如下：

考点名称：求反比例函数的解析式及反比例函数的应用

反比例函数解析式的确定方法：
由于在反比例函数关系式：y= 中，只有一个待定系数k，确定了k的值，也就确定了反比例函数。因此，只需给出一组x、y的对应值或图象上一点的坐标，代入中即可求出k的值，从而确定反比例函数的关系式。但在实际求反比例函数的解析式时，应该具体问题具体分析。

反比例函数的应用：
建立函数模型，解决实际问题。
用待定系数法求反比例函数关系式的一般步骤是：
①设所求的反比例函数为：y= (k≠0)；
②根据已知条件（自变量与函数的对应值）列出含k的方程；
③由代人法解待定系数k的值；
④把k值代人函数关系式y= 中。

反比例函数应用一般步骤：
①审题；
②求出反比例函数的关系式；
③求出问题的答案，作答。

http://www.00-edu.com/ks/shuxue/2/88/2019-04-10/997969.html十二生肖
十二星座