|
题文
已知:点P(a+1,a-1)关于x轴的对称点在反比例函数y= - (x>0)的图像上,y关于x的二次函数 (x>0)的图像上,y关于x的二次函数
y=k2x2-(2k+1)x+1的图像与坐标轴只有两个不同的交点A﹑B,求P点坐标和△PAB的面积。 |
题型:解答题 难度:中档
答案
解:(1)∵P点关于x轴的对称点为(a+1,-a+1)
它在 (x>0)图象上,且在第四象限 (x>0)图象上,且在第四象限
∴(a+1)(-a+1)=-8 ,即a2=9
∴a=3(a= -3舍去) ∴P(4,2)
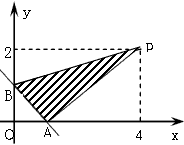
(2)当k=0时,y=-x+1,设一次函数图象与x轴交于A,与y轴交于B,
则A(1,0),B(0,1)
此时,S△PAB=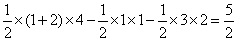
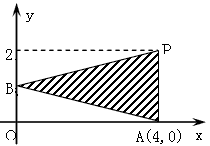
当k≠0时,函数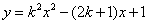 的图象为抛物线,与y轴交于B(0,1) 的图象为抛物线,与y轴交于B(0,1)
∵它的图象与坐标轴只有两个交点 ∴它的图象与x轴只有一个交点,设为A点
∴△=(2k+1)2- 4k2=0 解得:k=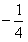
∴抛物线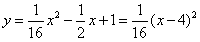 与x轴交于A(4,0) 与x轴交于A(4,0)
∴此时,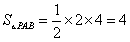
综合得:△PAB的面积为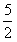 或4 或4 |
 | |
据专家权威分析,试题“已知:点P(a+1,a-1)关于x轴的对称点在反比例函数y=-(x>0)的图..”主要考查你对 求反比例函数的解析式及反比例函数的应用,求二次函数的解析式及二次函数的应用 等考点的理解。关于这些考点的“档案”如下:
求反比例函数的解析式及反比例函数的应用求二次函数的解析式及二次函数的应用
考点名称:求反比例函数的解析式及反比例函数的应用 考点名称:求二次函数的解析式及二次函数的应用
|

