零零教育信息网 首页 > 考试 > 数学 > 初中数学 > 求反比例函数的解析式及反比例函数的应用 > 正文 返回　打印

如图，已知一次函数y=kx+l（k≠0）的图象与x轴、y轴分别交于A、B两点，且与反比例函数y=的图象在第一象限交于C点，C点的横坐标为2。（1）求一次函数的解析式；（2）求△AOC的面积；（-九年级数学
[db:作者]  2019-04-13 00:00:00  互联网

题文

如图，已知一次函数y=kx+l（k≠0）的图象与x轴、y轴分别交于A、B两点，且与反比例函数y=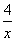的图象在第一象限交于C点，C点的横坐标为2。     
（1）求一次函数的解析式；   
（2）求△AOC的面积；     
（3）P是x轴上一动点，是否存在点P，使得由 A、P、C三点构成的三角形是直角三角形，若存在， 求出P点坐标；若不存在，请说明理由．

题型：解答题  难度：偏难

答案

解：（1）当x=2时，y==2   ∴C（2，2）
∴C在y=kx+1图象上，∴2k+1 =2，k=，∴y=x+1
（2）过C作CD上x轴于D（如图1）
当y=0时，y=x+1=0，得x= -2，则A（-2，0）
∴S△AOC=·OA·CD=×2×2=2
（3）存在点P，使得由A、P、C三点构成的三角形是直角三角形，有两种情况：
①若∠CPA =90°（如图2），则OP=2，P（2，0）
②若∠ACP =90°（如图3），∵A（-2，0），B（0，1），C（2，2）
∴AB=，AC=2，OA=2
∵ ∠ACP = ∠BOA=90°,  ∠BAO = ∠PAC,  ∴ △ABO ∽△APC 
∴   ∴ 解得AP=5
∴OP=3   ∴P（3，0）
综上所述，P点坐标（2，0）或（3，0）

据专家权威分析，试题“如图，已知一次函数y=kx+l（k≠0）的图象与x轴、y轴分别交于A、B两点..”主要考查你对  求反比例函数的解析式及反比例函数的应用，求一次函数的解析式及一次函数的应用，直角三角形的性质及判定  等考点的理解。关于这些考点的“档案”如下：

求反比例函数的解析式及反比例函数的应用求一次函数的解析式及一次函数的应用直角三角形的性质及判定

考点名称：求反比例函数的解析式及反比例函数的应用

  • 反比例函数解析式的确定方法：
    由于在反比例函数关系式 ：y= 中，只有一个待定系数k，确定了k的值，也就确定了反比例函数。因此，只需给出一组x、y的对应值或图象上一点的坐标，代入中即可求出k的值，从而确定反比例函数的关系式。但在实际求反比例函数的解析式时，应该具体问题具体分析。

    反比例函数的应用：
    建立函数模型，解决实际问题。

  • 用待定系数法求反比例函数关系式的一般步骤是：
    ①设所求的反比例函数为：y= (k≠0)；
    ②根据已知条件（自变量与函数的对应值）列出含k的方程；
    ③由代人法解待定系数k的值；
    ④把k值代人函数关系式y= 中。

    反比例函数应用一般步骤：
    ①审题；
    ②求出反比例函数的关系式；
    ③求出问题的答案，作答。

考点名称：求一次函数的解析式及一次函数的应用

  • 待定系数法求一次函数的解析式：
    先设出函数解析式，再根据条件确定解析式中的未知系数，从而得到函数的解析式的方法。

    一次函数的应用：
    应用一次函数解应用题，一般是先写出函数解析式，在依照题意，设法求解。
    （1）有图像的，注意坐标轴表示的实际意义及单位；
    （2）注意自变量的取值范围。

  • 用待定系数法求一次函数解析式的四个步骤：
    第一步（设）：设出函数的一般形式。（称一次函数通式）
    第二步（代）：代入解析式得出方程或方程组。
    第三步（求）：通过列方程或方程组求出待定系数k，b的值。
    第四步（写）：写出该函数的解析式。

    一次函数的应用涉及问题：
    一、分段函数问题
    分段函数是在不同区间有不同对应方式的函数，要特别注意自变量取值范围的划分，既要科学合理，又要符
    合实际。

    二、函数的多变量问题
    解决含有多变量问题时，可以分析这些变量的关系，选取其中一个变量作为自变量，然后根据问题的条件寻
    求可以反映实际问题的函数

    三、概括整合
    （1）简单的一次函数问题：①建立函数模型的方法；②分段函数思想的应用。
    （2）理清题意是采用分段函数解决问题的关键。

    生活中的应用：
    1.当时间t一定，距离s是速度v的一次函数。s=vt。
    2.如果水池抽水速度f一定，水池里水量g是抽水时间t的一次函数。设水池中原有水量S。g=S-ft。
    3.当弹簧原长度b（未挂重物时的长度）一定时，弹簧挂重物后的长度y是重物重量x的一次函数，即y=kx+b（k为任意正数）

  • 一次函数应用常用公式：
    1.求函数图像的k值：（y1-y2)/(x1-x2)
    2.求与x轴平行线段的中点：(x1+x2)/2
    3.求与y轴平行线段的中点：(y1+y2)/2
    4.求任意线段的长：√[(x1-x2)2+(y1-y2)2 ]
    5.求两个一次函数式图像交点坐标：解两函数式
    两个一次函数 y1=k1x+b1; y2=k2x+b2 令y1=y2 得k1x+b1=k2x+b2 将解得的x=x0值代回y1=k1x+b1 ; y2=k2x+b2 两式任一式 得到y=y0 则(x0,y0)即为 y1=k1x+b1 与 y2=k2x+b2 交点坐标
    6.求任意2点所连线段的中点坐标：[（x1+x2）/2，（y1+y2）/2]
    7.求任意2点的连线的一次函数解析式：（x-x1）/(x1-x2)=(y-y1)/(y1-y2) (若分母为0，则分子为0)
    （x,y）为 + ，+（正，正）时该点在第一象限
    （x,y）为 - ，+（负，正）时该点在第二象限
    （x,y）为 - ，-（负，负）时该点在第三象限
    （x,y）为 + ，-（正，负）时该点在第四象限
    8.若两条直线y1=k1x+b1//y2=k2x+b2，则k1=k2，b1≠b2
    9.如两条直线y1=k1x+b1⊥y2=k2x+b2，则k1×k2=-1
    10.
    y=k（x-n）+b就是直线向右平移n个单位
    y=k（x+n）+b就是直线向左平移n个单位
    y=kx+b+n就是向上平移n个单位
    y=kx+b-n就是向下平移n个单位
    口决：左加右减相对于x，上加下减相对于b。
    11.直线y=kx+b与x轴的交点：(-b/k，0) 与y轴的交点：(0，b)

考点名称：直角三角形的性质及判定

  • 直角三角形定义：
    有一个角为90°的三角形，叫做直角三角形。直角三角形可用Rt△表示，如直角三角形ABC写作Rt△ABC。

  • 直角三角形性质：
    直角三角形是一种特殊的三角形，它除了具有一般三角形的性质外，具有一些特殊的性质：
    性质1:直角三角形两直角边a，b的平方和等于斜边c的平方。即。如图，∠BAC=90°，则AB2+AC2=BC2（勾股定理)
    性质2:在直角三角形中，两个锐角互余。如图，若∠BAC=90°，则∠B+∠C=90°
    性质3：在直角三角形中，斜边上的中线等于斜边的一半（即直角三角形的外心位于斜边的中点，外接圆半径R=C/2）。
    性质4:直角三角形的两直角边的乘积等于斜边与斜边上高的乘积。
    性质5:

    如图，Rt△ABC中，∠BAC=90°，AD是斜边BC上的高，则有射影定理如下：
    （1）（AD)2=BD·DC。
    （2）（AB)2=BD·BC。
    （3）（AC)2=CD·BC。
    性质6:在直角三角形中，如果有一个锐角等于30°，那么它所对的直角边等于斜边的一半。
    在直角三角形中，如果有一条直角边等于斜边的一半，那么这条直角边所对的锐角等于30°。
    性质7:如图，1/AB2+1/AC2=1/AD2
    性质8:直角三角形被斜边上的高分成的两个直角三角形和原三角形相似。
    性质9：直角三角形直角上的角平分线与斜边的交点D 则    BD:DC=AB:AC

  • 直角三角形的判定方法：
    判定1：定义，有一个角为90°的三角形是直角三角形。
    判定2：判定定理：以a、b、c为边的三角形是以c为斜边的直角三角形。如果三角形的三边a，b，c满足，那么这个三角形就是直角三角形。（勾股定理的逆定理）。
    判定3：若一个三角形30°内角所对的边是某一边的一半，则这个三角形是以这条长边为斜边的直角三角形。
    判定4：两个锐角互为余角（两角相加等于90°）的三角形是直角三角形。
    判定5：若两直线相交且它们的斜率之积互为负倒数，则两直线互相垂直。那么
    判定6：若在一个三角形中一边上的中线等于其所在边的一半，那么这个三角形为直角三角形。
    判定7：一个三角形30°角所对的边等于这个三角形斜边的一半，则这个三角形为直角三角形。（与判定3不同，此定理用于已知斜边的三角形。）
http://www.00-edu.com/ks/shuxue/2/91/2019-04-13/1007392.html十二生肖
十二星座