题文
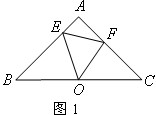
| 如图1所示,在△ABC中,AB=AC=2,∠A=90°,O为BC的中点,动点E在BA边上自由移动,动点F在AC边上自由移动. |
|
|
(1)点E,F的移动过程中,△OEF是否能成为∠EOF=45°的等腰三角形?若能,请指出△OEF为等腰三角形时动点E,F的位置.若不能,请说明理由;
(2)当∠EOF=45°时,设BE=x,CF=y,求y与x之间的函数解析式,写出x的取值范围;
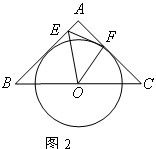
(3)在满足(2)中的条件时,若以O为圆心的圆与AB相切(如图2),试探究直线EF与⊙O的位置关系,并证明你的结论。 |
题型:解答题 难度:偏难
答案
解:(1)点E,F移动的过程中, 能成为 能成为 的等腰三角形 的等腰三角形
此时点的位置分别是:
①E是BA的中点,F与A重合
② ; ;
③E与A重合,F是AC的中点。
(2)在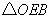 和 和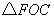 中 中
 , ,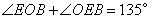
∴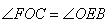
又∵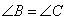
∴
∴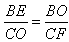
∵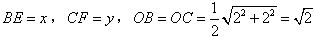
∴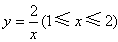 。 。
(3) 与 与 相切 相切
∵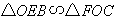
∴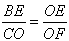
∴
即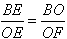
又∵
∴
∴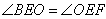
∴点O到AB和EF的距离相等
∵AB与 相切 相切
∴点O到EF的距离等于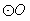 的半径 的半径
∴EF与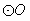 相切。 相切。 |
据专家权威分析,试题“如图1所示,在△ABC中,AB=AC=2,∠A=90°,O为BC的中点,动点E在BA..”主要考查你对 求反比例函数的解析式及反比例函数的应用,等腰三角形的性质,等腰三角形的判定,直线与圆的位置关系(直线与圆的相交,直线与圆的相切,直线与圆的相离) 等考点的理解。关于这些考点的“档案”如下:
求反比例函数的解析式及反比例函数的应用等腰三角形的性质,等腰三角形的判定直线与圆的位置关系(直线与圆的相交,直线与圆的相切,直线与圆的相离)
考点名称:求反比例函数的解析式及反比例函数的应用
考点名称:等腰三角形的性质,等腰三角形的判定
考点名称:直线与圆的位置关系(直线与圆的相交,直线与圆的相切,直线与圆的相离)

