零零教育信息网 首页 > 考试 > 数学 > 初中数学 > 方差 > 正文 返回　打印

在某区的一条小路上，有一些断断续续的台阶，如图是其中的甲、乙两段台阶路的示意图，图中数据（单位：cm）是每级台阶的高度．甲路段数据的方差为S甲2=23，乙路段数据的方差为S乙-数学
[db:作者]  2019-04-14 00:00:00  零零社区

题文

在某区的一条小路上，有一些断断续续的台阶，如图是其中的甲、乙两段台阶路的示意图，图中数据（单位：cm）是每级台阶的高度．甲路段数据的方差为S甲2=
2
3
，乙路段数据的方差为S乙2=
35
3
，请用所学过的有关统计知识（平均数、中位数、方差和极差）回答下列问题：
（1）分别求出两段台阶数据的平均数、中位数和极差；
（2）哪段路走起来更舒服？为什么？
（3）为方便游客行走，需要重新整修台阶，在台阶数不变情况下，请你对每梯台阶的高度提出合理的整修建议．


题型：解答题  难度：中档

答案

（1）甲路段平均数=
15+16+16+14+14+15
6
=15，
中位数=15，极差=2；
乙路段平均数=
11+15+18+17+10+19
6
=15，
中位数=16，极差=9；

（2）甲路段走起来更舒服些．
∵S甲2＜S乙2
∴甲路段波动小；

（3）根据平均数以及当方差最小时数据无波动，建议每步台阶都修为高15cm．

据专家权威分析，试题“在某区的一条小路上，有一些断断续续的台阶，如图是其中的甲、乙..”主要考查你对  方差  等考点的理解。关于这些考点的“档案”如下：

方差

考点名称：方差

  • 方差:
    是各个数据与平均数之差的平方和的平均数。
    在概率论和数理统计中，方差用来度量随机变量和其数学期望（即均值）之间的偏离程度。
    在许多实际问题中，研究随机变量和均值之间的偏离程度有着很重要的意义。
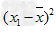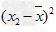    设有n个数据各数据x1，x2，…，xn各数据与它们的平均数的差的平方分别是，，…，，我们用它的平均数，即用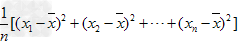来衡量这组数据的波动大小，并把它叫做这组数据的方差，记作。

  • 方差特点:
    （1）设c是常数，则D(c)=0。
    （2）设X是随机变量，c是常数，则有D(cX)=(c2)D(X)。
    （3）设 X 与 Y 是两个随机变量，则
    D(X+Y)= D(X)+D(Y)+2E{[X-E(X)][Y-E(Y)]}
    特别的，当X，Y是两个相互独立的随机变量，上式中右边第三项为0（常见协方差），
    则D(X+Y)=D(X)+D(Y)。此性质可以推广到有限多个相互独立的随机变量之和的情况。
    （4）D(X)=0的充分必要条件是X以概率为1取常数值c，即P{X=c}=1，其中E(X)=c。
    （5）D（aX+bY）=a^2DX+b^2DY+2abE{[X-E(X)][Y-E(Y)]}。

    意义：
    在样本容量相同的情况下，方差越大，说明数据的波动越大，越不稳定。

    标准差：
    方差的算术平均根，即，并把它叫做这组数据的标准差，它也是一个用来衡量一组数据的波动大小的重要的量。

  • 公式:
    方差是实际值与期望值之差平方的期望值，而标准差是方差算术平方根。 在实际计算中，我们用以下公式计算方差。
    方差是各个数据与平均数之差的平方的平均数,即s^2=(1/n)[(x1-x_)^2+(x2-x_)^2+...+(xn-x_)^2]，其中，x_表示样本的平均数，n表示样本的数量，^，xn表示个体，而s^2就表示方差。
    而当用(1/n)[(x1-x_)^2+(x2-x_)^2+...+(xn-x_)^2]作为样本X的方差的估计时，发现其数学期望并不是X的方差，而是X方差的(n-1)/n倍，[1/(n-1)][(x1-x_)^2+(x2-x_)^2+...+(xn-x_)^2]的数学期望才是X的方差，用它作为X的方差的估计具有“无偏性”，所以我们总是用[1/(n-1)]∑(xi-X~)^2来估计X的方差，并且把它叫做“样本方差”。
    方差，通俗点讲，就是和中心偏离的程度！用来衡量一批数据的波动大小（即这批数据偏离平均数的大小）并把它叫做这组数据的方差。记作S&sup2.在样本容量相同的情况下，方差越大，说明数据的波动越大，越不稳定。

    方差分析主要用途：
    ①均数差别的显著性检验;
    ②分离各有关因素并估计其对总变异的作用;
    ③分析因素间的交互作用;
    ④方差齐性检验。
http://www.00-edu.com/ks/shuxue/2/95/2019-04-14/1030364.html十二生肖
十二星座