零零教育信息网 首页 > 考试 > 数学 > 初中数学 > 一元二次方程的解法 > 正文 返回　打印

如图，已知直线AB与x轴、y轴分别交于A和B，OA=4，且OA、OB长是关于x的方程x2-mx+12=0的两实根，以OB为直径的⊙M与AB交于C，连接CM并延长交x轴于N。（1）求⊙M的半径。（2）求线段A-九年级数学
[db:作者]  2019-04-27 00:00:00  互联网

题文

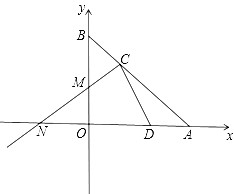
如图，已知直线AB与x轴、y轴分别交于A和B，OA=4，且OA、OB长是关于x的方程x2-mx+12=0的两实根，以OB为直径的⊙M与AB交于C，连接CM并延长交x轴于N。

（1）求⊙M的半径。
（2）求线段AC的长。
（3）若D为OA的中点，求证：CD是⊙M的切线。
题型：解答题  难度：偏难

答案

解：（1）∵OA=4
∴A（4，0）
又OA·OB长是x2-mx+12=0的两根
∴OA·OB=1
2∴OB=3
故B（0，3）
∵OB为直径
∴半径MB=；
（2）连接OC
∵OB是⊙M直径
∴OC⊥BC
∴OC·AB=OA·OB
∵AB==5
∴OC·5=3·4
∴OC=
∴AC==。
（3）∵OM=OC
∴∠MOC=∠MCO
又CD是Rt△OCA斜边上中线
∴DC=DO
∴∠DOC=∠DCO
∵∠DOC+∠MOC=90°
∴∠MCO+∠DCO=90°
∴DC⊥MC
∴CD是⊙M的切线。

据专家权威分析，试题“如图，已知直线AB与x轴、y轴分别交于A和B，OA=4，且OA、OB长是关..”主要考查你对  一元二次方程的解法，勾股定理，直线与圆的位置关系（直线与圆的相交，直线与圆的相切，直线与圆的相离）  等考点的理解。关于这些考点的“档案”如下：

一元二次方程的解法勾股定理直线与圆的位置关系（直线与圆的相交，直线与圆的相切，直线与圆的相离）

考点名称：一元二次方程的解法

  • 一元二次方程的解：
    能够使方程左右两边相等的未知数的值叫做方程的解。
    解一元二次方程方程：
    求一元二次方程解的过程叫做解一元二次方程方程。

  • 韦达定理：
    一元二次方程根与系数的关系（以下两个公式很重要，经常在考试中运用到）
    一般式：ax2+bx+c=0的两个根x1和x2关系：
    x1+x2= -b/a
    x1·x2=c/a

  • 一元二次方程的解法：
    1、直接开平方法
    利用平方根的定义直接开平方求一元二次方程的解的方法叫做直接开平方法。
    直接开平方法适用于解形如的一元二次方程，根据平方根的定义可知，x+a 是b的平方根，当时，；当b<0时，方程没有实数根。
    用直接开平方法求一元二次方程的根，一定要正确运用平方根的性质，即正数的平方根有两个，它们互为相反数，零的平方根是零，负数没有平方根。

    2、配方法
    配方法是一种重要的数学方法，它不仅在解一元二次方程上有所应用，而且在数学的其他领域也有着广泛的应用。
    配方法的理论根据是完全平方公式，把公式中的a看做未知数x，并用x代替，则有 。

    3、公式法
    公式法是用求根公式解一元二次方程的解的方法，它是解一元二次方程的一般方法。
    一元二次方程 的求根公式：
    求根公式是专门用来解一元二次方程的，故首先要求a≠0；有因为开平方运算时，被开方数必须是非负数，所以第二个条件是b2-4ac≥0。即求根公式使用的前提条件是a≠0且b2-4ac≥0。

    4、因式分解法
    因式分解法就是利用因式分解的手段，求出方程的解的方法，这种方法简单易行，是解一元二次方程最常用的方法。

考点名称：勾股定理

  • 勾股定理:
    直角三角形两直角边(即“勾”，“股”)边长平方和等于斜边(即“弦”)边长的平方。也就是说，如果直角三角形的两直角边长分别为a，b，斜边长为c，那么。
    勾股定理只适用于直角三角形，应用于解决直角三角形中的线段求值问题。

  • 定理作用
    ⑴勾股定理是联系数学中最基本也是最原始的两个对象——数与形的第一定理。
    ⑵勾股定理导致不可通约量的发现，从而深刻揭示了数与量的区别，即所谓“无理数"与有理数的差别，这就是所谓第一次数学危机。
    ⑶勾股定理开始把数学由计算与测量的技术转变为证明与推理的科学。
    ⑷勾股定理中的公式是第一个不定方程，也是最早得出完整解答的不定方程，它一方面引导到各式各样的不定方程，包括著名的费尔马大定理，另一方面也为不定方程的解题程序树立了一个范式。

  • 勾股定理的应用：
    数学
    从勾股定理出发开平方、开立方、求圆周率等，运用勾股定理数学家还发现了无理数。
    勾股定理在几何学中的实际应用非常广泛，较早的应用案例有《九章算术》中的一题：“今有池，芳一丈，薛生其中央，出水一尺，引薛赴岸，适与岸齐，问水深几何？答曰："一十二尺"。

    生活
    勾股定理在生活中的应用也较广泛，举例说明如下：
    1、挑选投影设备时需要选择最佳的投影屏幕尺寸。以教室为例，最佳的屏幕尺寸主要取决于使用空间的面积，从而计划好学生座位的多少和位置的安排。选购的关键则是选择适合学生的屏幕而不是选择适合投影机的屏幕，也就是说要把学生的视觉感受放在第一位。一般来说在选购时可参照三点：
    第一，屏幕高度大约等于从屏幕到学生最后一排座位的距离的1/6；
    第二，屏幕到第一排座位的距离应大于2倍屏幕的高度；
    第三，屏幕底部应离观众席所在地面最少122厘米。
    屏幕的尺寸是以其对角线的大小来定义的。一般视频图像的宽高比为4:3，教育幕为正方形。如一个72英寸的屏幕，根据勾股定理，很快就能得出屏幕的宽为1.5m，高为1.1m。
    2、2005年珠峰高度复测行动。
    测量珠峰的一种方法是传统的经典测量方法，就是把高程引到珠峰脚下，当精确高程传递至珠峰脚下的6个峰顶交会测量点时，通过在峰顶竖立的测量觇标，运用“勾股定理”的基本原理测定珠峰高程，配合水准测量、三角测量、导线测量等方式，获得的数据进行重力、大气等多方面改正计算，最终得到珠峰高程的有效数据。
    通俗来说，就是分三步走：
    第一步，先在珠峰脚下选定较容易的、能够架设水准仪器的测量点，先把这些点的精确高程确定下来；
    第二步，在珠峰峰顶架起觇标，运用三角几何学中“勾股定理”的基本原理，推算出珠峰峰顶相对于这几个点的高程差；
    第三步，获得的高程数据要进行重力、大气等多方面的改正计算，最终确定珠峰高程测量的有效数据。

考点名称：直线与圆的位置关系（直线与圆的相交，直线与圆的相切，直线与圆的相离）

  • 直线与圆的位置关系:
    直线与圆的位置关系有三种：直线与圆相交，直线与圆相切，直线与圆相离。
    （1）相交：直线和圆有两个公共点时，叫做直线和圆相交，这时直线叫做圆的割线，公共点叫做交点AB与⊙O相交，d<r；
    （2）相切：直线和圆有唯一公共点时，叫做直线和圆相切，这时直线叫做圆的切线，这个唯一的公共点叫做切点。AB与⊙O相切，d=r。
    （3）相离：直线和圆没有公共点时，叫做直线和圆相离,AB与圆O相离，d>r。（d为圆心到直线的距离）

  • 直线与圆的三种位置关系的判定与性质：
    （1）数量法：通过比较圆心O到直线距离d与圆半径的大小关系来判定，
    如果⊙O的半径为r，圆心O到直线l的距离为d，则有：
    直线l与⊙O相交d<r；
    直线l与⊙O相切d=r；
    直线l与⊙O相离d>r；
    （2）公共点法：通过确定直线与圆的公共点个数来判定。
    直线l与⊙O相交d<r2个公共点；
    直线l与⊙O相切d=r有唯一公共点；
    直线l与⊙O相离d>r无公共点 。

    圆的切线的判定和性质   
    （1）切线的判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线。
    （2）切线的性质定理：圆的切线垂直于经过切点的半径。

    切线长：
    在经过圆外一点的圆的切线上，这点和切点之间的线段的长叫做这点到圆的切线长。
    切线长定理：
    从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角。

  • 直线与圆的位置关系判定方法:
    平面内，直线Ax+By+C=0与圆x2+y2+Dx+Ey+F=0的位置关系判断一般方法是：
    1.由Ax+By+C=0，可得y=（-C-Ax）/B，（其中B不等于0），代入x2+y2+Dx+Ey+F=0，即成为一个关于x的方程
    如果b2-4ac>0，则圆与直线有2交点，即圆与直线相交。
    如果b2-4ac=0，则圆与直线有1交点，即圆与直线相切。
    如果b2-4ac<0，则圆与直线有0交点，即圆与直线相离。

    2.如果B=0即直线为Ax+C=0，即x=-C/A，它平行于y轴（或垂直于x轴），将x2+y2+Dx+Ey+F=0化为（x-a）2+（y-b）2=r2。
    令y=b，求出此时的两个x值x1、x2，并且规定x1<x2，那么： 
    当x=-C/A<x1或x=-C/A>x2时，直线与圆相离；
    当x1<x=-C/A<x2时，直线与圆相交。 
http://www.00-edu.com/ks/shuxue/2/107/2019-04-27/1086332.html十二生肖
十二星座