在等边三角形、矩形、菱形、等腰梯形中任选一个图形，下列说法正确的是（）A．选的图形是旋转对称图形、中心对称图形的概率一样大B．选的图形是轴对称图形是确定事件C．选的图形是-数学打印页面

在等边三角形、矩形、菱形、等腰梯形中任选一个图形，下列说法正确的是（）A．选的图形是旋转对称图形、中心对称图形的概率一样大B．选的图形是轴对称图形是确定事件C．选的图形是-数学

[db:作者] 2019-05-10 00:00:00 互联网

题文

在等边三角形、矩形、菱形、等腰梯形中任选一个图形，下列说法正确的是（　　）
A．选的图形是旋转对称图形、中心对称图形的概率一样大
B．选的图形是轴对称图形是确定事件
C．选的图形是轴对称图形但不是中心对称图形的概率是
1
4
D．选的图形是中心对称图形的概率为
3
4
题型：单选题难度：偏易

答案

A、四个图形中中心对称图形有矩形、菱形两个，旋转对称图形有四个，故两个概率不一样大，故错误；
B、所有图形都是轴对称图形，故选的图形是轴对称图形是确定事件，故正确；
C、是轴对称但不是中心对称的图形有两个，概率为
1
2
，故错误；
D、是中心对称图形的有2个，概率为
1
2
，故错误，
故选B．

据专家权威分析，试题“在等边三角形、矩形、菱形、等腰梯形中任选一个图形，下列说法正..”主要考查你对概率的意义，轴对称，中心对称，图形旋转等考点的理解。关于这些考点的“档案”如下：

概率的意义轴对称中心对称图形旋转

考点名称：概率的意义

概率的意义：
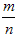一般地，在大量重复试验中，如果事件A发生的频率会稳定在某个常数p附近，那么这个常数p就叫做事件A的概率，记作P（A）=p，概率从某种数量上刻画一个不确定事件发生的可能性的大小。
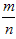事件和概率的表示方法：一般地，事件用英文大写字母A，B，C，…，表示事件A的概率p，可记为P（A）=P。
事件的概率：必然事件的概率为1，不可能事件的概率为0，随机事件A的概率为0<P（A）<1。
注：（1）在n试验中，事件A发生的频率m满足0≤m≤n，所以0≤≤1，故0≤P（A）≤1；
（2）P（A）=0表示事件A是不可能发生的事件，P（A）=1表示事件A是必然发生的事件；
（3）概率越大，表示事件发生的可能性越大；概率越小，表示事件发生的可能性越小；
（4）人们通常对随机事件进行大量的反复试验来研究概率，一般大量试验事件发生的频率可作为概率的估计值。

考点名称：轴对称

轴对称的定义：
把一个图形沿着某一条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线对称，这条直线叫做对称轴，折叠后重合的点是对应点,叫做对称点。轴对称和轴对称图形的特性是相同的，对应点到对称轴的距离都是相等的。
轴对称的性质：
（1）对应点所连的线段被对称轴垂直平分；
（2）对应线段相等，对应角相等；
（3）关于某直线对称的两个图形是全等图形。
轴对称的判定：
如果两个图形的对应点连线被同一条直线垂直平分，那么这两个图形关于这条直线对称。
这样就得到了以下性质：
1.如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线。
2.类似地，轴对称图形的对称轴，是任何一对对应点所连线段的垂直平分线。
3.线段的垂直平分线上的点与这条线段的两个端点的距离相等。　
4.对称轴是到线段两端距离相等的点的集合。

轴对称作用:
可以通过对称轴的一边从而画出另一边。
可以通过画对称轴得出的两个图形全等。
扩展到轴对称的应用以及函数图像的意义。

轴对称的应用:
关于平面直角坐标系的X,Y对称意义
如果在坐标系中，点A与点B关于直线X对称，那么点A的横坐标不变，纵坐标为相反数。
相反的,如果有两点关于直线Y对称,那么点A的横坐标为相反数,纵坐标不变。

关于二次函数图像的对称轴公式(也叫做轴对称公式 )
设二次函数的解析式是 y=ax²+bx+c
则二次函数的对称轴为直线 x=-b/2a,顶点横坐标为 -b/2a,顶点纵坐标为 (4ac-b²)/4a

在几何证题、解题时，如果是轴对称图形，则经常要添设对称轴以便充分利用轴对称图形的性质。
譬如，等腰三角形经常添设顶角平分线；
矩形和等腰梯形问题经常添设对边中点连线和两底中点连线；
正方形，菱形问题经常添设对角线等等。
另外，如果遇到的图形不是轴对称图形，则常选择某直线为对称轴，补添为轴对称图形，
或将轴一侧的图形通过翻折反射到另一侧，以实现条件的相对集中。

考点名称：中心对称

中心对称的定义：
把一个图形绕着某一个点旋转180°，如果它能够与另一个图形重合，那么说这两个图形关于这个点中心对称，这个点叫做对称中心。
中心对称图形的定义：
在平面内，一个图形绕着某一个点旋转180°，如果旋转前后的图形互相重合，那么这个图形叫做中心对称图形，这个点就是它的对称中心。
中心对称的性质：
①关于中心对称的两个图形是全等形。
②关于中心对称的两个图形，对称点连线都经过对称中心，并且被对称中心平分。
③关于中心对称的两个图形，对应线段平行（或在同一直线上）且相等。

中心对称的判定：
如果两个图形的对应点连线都经过某一点，并且被这一点平分，那么这两个图形关于这一点对称。
中心对称与中心对称图形的联系:
中心对称和中心对称图形是两个不同而又紧密联系的概念。
区别是：
中心对称是指两个全等图形之间的相互位置关系，这两个图形关于一点对称，这个点是对称中心，两个图形关于点的对称也叫做中心对称。成中心对称的两个图形中，其中一个图形上所有点关于对称中心的对称点都在另一个图形上，反之，另一个图形上所有点的对称点，又都在这个图形上；
而中心对称图形是指一个图形本身成中心对称。中心对称图形上所有点关于对称中心的对称点都在这个图形本身上。如果将中心对称的两个图形看成一个整体（一个图形），那么这个图形就是中心对称图形；一个中心对称图形，如果把对称的部分看成是两个图形，那么它们又是关于中心对称。
也就是说：
① 中心对称图形：如果把一个图形绕某一点旋转180度后能与自身重合，这个图形是中心对称图形。
②中心对称：如果把一个图形绕某一点旋转180度后能与另一个图形重合，这两个图形成中心对称。

考点名称：图形旋转

定义：
在平面内，将一个图形绕一点按某个方向转动一个角度，这样的运动叫做图形的旋转。这个定点叫做旋转中心，转动的角度叫做旋转角。
图形的旋转是图形上的每一点在平面上绕着某个固定点旋转固定角度的位置移动，其中对应点到旋转中心的距离相等，对应线段的长度、对应角的大小相等，旋转前后图形的大小和形状没有改变。
图形旋转性质：
（1）对应点到旋转中心的距离相等。
（2）对应点与旋转中心所连线段的夹角等于旋转角。
旋转对称中心
把一个图形绕着一个点旋转一定的角度后，与原来的图形相吻合，这种图形叫做旋转对称图形，这个定点叫做旋转对称中心，旋转的角度叫做旋转角。（旋转角大于0°小于360°）

http://www.00-edu.com/ks/shuxue/2/113/2019-05-10/1116589.html十二生肖
十二星座