零零教育信息网 首页 > 考试 > 数学 > 初中数学 > 概率的意义 > 正文 返回　打印

历史上，雅各布．伯努利等人通过大量投掷硬币的实验，验证了“正面向上的频率在0.5左右摆动，那么投掷一枚硬币10次，下列说法正确的是（）A．“正面向上”必会出现5次B．“反面向上”-数学
[db:作者]  2019-05-10 00:00:00  零零社区

题文

历史上，雅各布．伯努利等人通过大量投掷硬币的实验，验证了“正面向上的频率在0.5左右摆动，那么投掷一枚硬币10次，下列说法正确的是（　　）
A．“正面向上”必会出现5次
B．“反面向上”必会出现5次
C．“正面向上”可能不出现
D．“正面向上”与“反面向上”出现的次数必定一样，但不一定是5次
题型：单选题  难度：偏易

答案

A、“正面向上”不一定会出现5次，故本选项错误；
B、“反面向上”不一定会出现5次，故本选项错误；
C、“正面向上”可能不出现，只是几率不太大，故本选项正确；
D、“正面向上”与“反面向上”出现的次数可能不一样，故本选项错误；
故选C．

据专家权威分析，试题“历史上，雅各布．伯努利等人通过大量投掷硬币的实验，验证了“正面..”主要考查你对  概率的意义，利用频率估算概率  等考点的理解。关于这些考点的“档案”如下：

概率的意义利用频率估算概率

考点名称：概率的意义

  • 概率的意义：
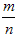    一般地，在大量重复试验中，如果事件A发生的频率会稳定在某个常数p附近，那么这个常数p就叫做事件A的概率，记作P（A）=p，概率从某种数量上刻画一个不确定事件发生的可能性的大小。
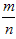    事件和概率的表示方法：一般地，事件用英文大写字母A，B，C，…，表示事件A的概率p，可记为P（A）=P。
    事件的概率：必然事件的概率为1，不可能事件的概率为0，随机事件A的概率为0<P（A）<1。
    注：（1）在n试验中，事件A发生的频率m满足0≤m≤n，所以0≤≤1，故0≤P（A）≤1；
    （2）P（A）=0表示事件A是不可能发生的事件，P（A）=1表示事件A是必然发生的事件；
    （3）概率越大，表示事件发生的可能性越大；概率越小，表示事件发生的可能性越小；
    （4）人们通常对随机事件进行大量的反复试验来研究概率，一般大量试验事件发生的频率可作为概率的估计值。

考点名称：利用频率估算概率

  • 在同样条件下，做大量的重复试验，利用一个随机事件发生的频率逐渐稳定到某个常数，可以估计这个事件发生的概率。
    注：
    （1）当试验的可能结果不是有限个，或各种结果发生的可能性不相等时，一般用统计频率的方法来估计概率；
    （2）利用频率估计概率的数学依据是大数定律：当试验次数很大时，随机事件A出现的频率，稳定地在某个数值P附近摆动.这个稳定值P，叫做随机事件A的概率，并记为P(A)=P。
    （3）利用频率估计出的概率是近似值。



http://www.00-edu.com/ks/shuxue/2/113/2019-05-10/1116611.html十二生肖
十二星座