共有4条线段，长度分别为1cm，2cm，3cm，4cm，任取其中的3条，恰能构成三角形的概率为______．-数学打印页面

共有4条线段，长度分别为1cm，2cm，3cm，4cm，任取其中的3条，恰能构成三角形的概率为______．-数学

[db:作者] 2019-05-10 00:00:00 互联网

题文

共有4条线段，长度分别为1cm，2cm，3cm，4cm，任取其中的3条，恰能构成三角形的概率为______．
题型：填空题难度：中档

答案

因为共有4条线段，任取其中的3条，共4种取法，能构成三角形只有2cm，3cm，4cm，一种情况，
故恰能构成三角形的概率为
1
4
．

据专家权威分析，试题“共有4条线段，长度分别为1cm，2cm，3cm，4cm，任取其中的3条，恰..”主要考查你对概率的意义，三角形的三边关系等考点的理解。关于这些考点的“档案”如下：

概率的意义三角形的三边关系

考点名称：概率的意义

概率的意义：
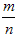一般地，在大量重复试验中，如果事件A发生的频率会稳定在某个常数p附近，那么这个常数p就叫做事件A的概率，记作P（A）=p，概率从某种数量上刻画一个不确定事件发生的可能性的大小。
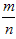事件和概率的表示方法：一般地，事件用英文大写字母A，B，C，…，表示事件A的概率p，可记为P（A）=P。
事件的概率：必然事件的概率为1，不可能事件的概率为0，随机事件A的概率为0<P（A）<1。
注：（1）在n试验中，事件A发生的频率m满足0≤m≤n，所以0≤≤1，故0≤P（A）≤1；
（2）P（A）=0表示事件A是不可能发生的事件，P（A）=1表示事件A是必然发生的事件；
（3）概率越大，表示事件发生的可能性越大；概率越小，表示事件发生的可能性越小；
（4）人们通常对随机事件进行大量的反复试验来研究概率，一般大量试验事件发生的频率可作为概率的估计值。

考点名称：三角形的三边关系

三角形的三边关系：
在三角形中，任意两边和大于第三边，任意两边差小于第三边。
设三角形三边为a,b,c
则
a+b>c
a+c>b
b+c>a
a-b<c
a-c<b
b-c<a
在直角三角形中，设a、b为直角边，c为斜边。
则两直角边的平方和等于斜边平方。
在等边三角形中，a=b=c
在等腰三角形中， a,b为两腰，则a=b
在三角形ABC的内角A、B、C所对边分别为a、b、c的情况下，c²=a²+b²-2abcosc
三角形的三边关系定理及推论：
（1）三角形三边关系定理：三角形的两边之和大于第三边。
推论：三角形的两边之差小于第三边。
（2）三角形三边关系定理及推论的作用：
①判断三条已知线段能否组成三角形；
②当已知两边时，可确定第三边的范围；
③证明线段不等关系。

http://www.00-edu.com/ks/shuxue/2/113/2019-05-10/1116654.html十二生肖
十二星座