在一次晚会上，大家围着飞镖游戏前。只见靶子设计成如图形式。已知从里到外的三个圆的半径分别为l，2，3，并且形成A，B，C三个区域。如果飞镖没有停落在最大圆内或只停落在圆-九年级数学打印页面

在一次晚会上，大家围着飞镖游戏前。只见靶子设计成如图形式。已知从里到外的三个圆的半径分别为l，2，3，并且形成A，B，C三个区域。如果飞镖没有停落在最大圆内或只停落在圆-九年级数学

[db:作者] 2019-05-18 00:00:00 互联网

题文

在一次晚会上，大家围着飞镖游戏前。只见靶子设计成如图形式。已知从里到外的三个圆的半径分别为l，2，3，并且形成A，B，C三个区域。如果飞镖没有停落在最大圆内或只停落在圆周上，那么可以重新投镖。
（1）分别求出三个区域的面积；
（2）雨薇与方冉约定：飞镖停落在A、B区域雨薇得1分，飞镖落在C区域方冉得1分。你认为这个游戏公平吗? 为什么? 如果不公平，请你修改得分规则，使这个游戏公平。

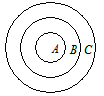题型：解答题难度：中档

答案

解：（1）S_A=π·1²=π，S_B=π·2²-π·1²=3π，S_C=π·3²-π·2²=5π
（2）P(A)==，P(B)= =，P(C)=
P(雨薇得分)=，
P(方冉得分)=
∵P(雨薇得分)≠P(方冉得分)
∴这个游戏不公平。
修改得分规则：飞镖停落在A区域得2分，飞镖停落在B区域、C区域得1分，这样游戏就公平了。

据专家权威分析，试题“在一次晚会上，大家围着飞镖游戏前。只见靶子设计成如图形式。已..”主要考查你对列举法求概率，圆和圆的位置关系（圆和圆的相离，圆与圆的相交，圆与圆的相切）等考点的理解。关于这些考点的“档案”如下：

列举法求概率圆和圆的位置关系（圆和圆的相离，圆与圆的相交，圆与圆的相切）

考点名称：列举法求概率

可能条件下概率的意义：一般地，如果在一次试验中，有n种可能的结果，并且它们发生的可能性都相等，事件A包含其中的m中结果，那么事件A发生的概率为P（A）=。
等可能条件下概率的特征：
（1）对于每一次试验中所有可能出现的结果都是有限的；
（2）每一个结果出现的可能性相等。
概率的计算方法：
（1）列举法（列表或画树状图），
（2）公式法；
列表法或树状图这两种举例法，都可以帮助我们不重不漏的列出所以可能的结果。

列表法
（1）定义：用列出表格的方法来分析和求解某些事件的概率的方法叫做列表法。
（2）列表法的应用场合
当一次试验要设计两个因素，并且可能出现的结果数目较多时，为不重不漏地列出所有可能的结果，通常采用列表法。

树状图法
（1）定义：通过列树状图列出某事件的所有可能的结果，求出其概率的方法叫做树状图法。
（2）运用树状图法求概率的条件
当一次试验要设计三个或更多的因素时，用列表法就不方便了，为了不重不漏地列出所有可能的结果，通常采用树状图法求概率。

考点名称：圆和圆的位置关系（圆和圆的相离，圆与圆的相交，圆与圆的相切）

圆和圆的位置关系：
如果两个圆没有公共点，那么就说这两个圆相离，相离分为外离和内含两种。
如果两个圆只有一个公共点，那么就说这两个圆相切，相切分为外切和内切两种。
如果两个圆有两个公共点，那么就说这两个圆相交。

圆心距：两圆圆心的距离叫做两圆的圆心距。
圆和圆位置关系的性质与判定：
设两圆的半径分别为R和r，圆心距为d，那么
两圆外离d>R+r（没有交点）
两圆外切d=R+r （有一个交点，叫切点）
两圆相交R-r<d<R+r（R≥r）(有两个交点)
两圆内切d=R-r（R>r） (有一个交点,叫切点)
两圆内含d<R-r（R>r）(没有交点)

两圆相切的性质：
（1）连心线：两圆圆心的连线。
（2）两圆相切的性质：相切两圆的连心线必过切点，即两圆圆心、切点三点在一条直线上。

http://www.00-edu.com/ks/shuxue/2/114/2019-05-18/1122926.html十二生肖
十二星座