|
题文
已知抛物线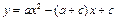 (其中a ≠ c且a ≠0). (其中a ≠ c且a ≠0).
(1)求此抛物线与x轴的交点坐标;(用a,c的代数式表示)
(2)若经过此抛物线顶点A的直线 与此抛物线的另一个交点为 与此抛物线的另一个交点为 , ,
求此抛物线的解析式;
(3)点P在(2)中x轴上方的抛物线上,直线 与 y轴的交点为C,若 与 y轴的交点为C,若
 ,求点P的坐标; ,求点P的坐标;
(4)若(2)中的二次函数的自变量x在n≤x< (n为正整数)的范围内取值时,记它的整数函数值的个数为N, 则N关于n的函数关系式为 . (n为正整数)的范围内取值时,记它的整数函数值的个数为N, 则N关于n的函数关系式为 . |
题型:解答题 难度:中档
答案
解:(1)抛物线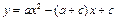 与x轴交点的横坐标是关于x的方程 与x轴交点的横坐标是关于x的方程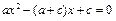 (其中a ≠ 0,a ≠c)的解. (其中a ≠ 0,a ≠c)的解.
解得 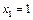 , , . ………………………………………………………… 1分 . ………………………………………………………… 1分
∴ 抛物线与x轴交点的坐标为 , , .……………………………… 2分 .……………………………… 2分
(2)抛物线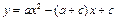 的顶点A的坐标为 的顶点A的坐标为 . .
∵ 经过此抛物线顶点A的直线 与此抛物线的另一个交点为 与此抛物线的另一个交点为 , ,

由③得 c ="0. " ……………………………………………………………3分
将其代入①、② 得 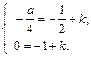
解得 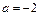 . .
∴ 所求抛物线的解析式为 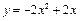 .…………………………………… 4分 .…………………………………… 4分
(3)作PE⊥x轴于点E, PF⊥y轴于点F.(如图7)

抛物线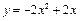 的顶点A的坐标 的顶点A的坐标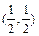 , ,
点B的坐标为 ,点C的坐标为 ,点C的坐标为 . .
设点P的坐标为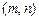 . .
∵ 点P在x轴上方的抛物线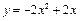 上, 上,
∴ 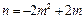 ,且0<m<1, ,且0<m<1, . .
∴ 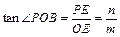 , ,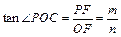 . .
∵  , ,
∴  . .
解得 m=2n,或 (舍去). ………………………………………………5分 (舍去). ………………………………………………5分
将m=2n代入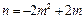 ,得 ,得 . .
解得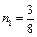 , ,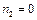 (舍去). (舍去).
∴  . .
∴ 点P的坐标为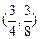 . …………………………………………………………6分 . …………………………………………………………6分
(4)N关于n的函数关系式为N="4n" . ………………………………………………7分
说明:二次函数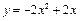 的自变量x在n≤x< 的自变量x在n≤x< (n为正整数)的范围内取值,此时y随x的增大而减小, (n为正整数)的范围内取值,此时y随x的增大而减小,
∴ <y≤ <y≤ , ,
其中的整数有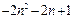 , ,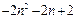 ,… ,… . .
 . . |
据专家权威分析,试题“已知抛物线(其中a≠c且a≠0).(1)求此抛物线与x轴的交点坐标;(用a..”主要考查你对 二次函数的定义,二次函数的图像,二次函数的最大值和最小值,求二次函数的解析式及二次函数的应用 等考点的理解。关于这些考点的“档案”如下:
二次函数的定义二次函数的图像二次函数的最大值和最小值求二次函数的解析式及二次函数的应用
考点名称:二次函数的定义 考点名称:二次函数的图像 考点名称:二次函数的最大值和最小值 考点名称:求二次函数的解析式及二次函数的应用
|

