|
题文
(本题满分12分)在平面直角坐标系中,抛物线交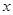 轴于 轴于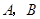 两点,交 两点,交 轴于点 轴于点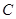 ,已知抛物线的对称轴为 ,已知抛物线的对称轴为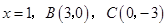 . .
小题1:⑴求这个抛物线的解析式;
小题2:⑵在抛物线的对称轴上是否存在一点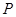 ,使点 ,使点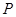 到A、C两点间的距离之和最大.若存在,求出点 到A、C两点间的距离之和最大.若存在,求出点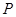 的坐标;若不存在,请说明理由. 的坐标;若不存在,请说明理由.
小题3:(3)如果在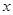 轴上方平行于 轴上方平行于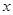 轴的一条直线交抛物线于 轴的一条直线交抛物线于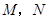 两点,以 两点,以 为直径作圆恰好与 为直径作圆恰好与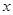 轴相切,求此圆的直径. 轴相切,求此圆的直径. |
题型:解答题 难度:中档
答案
小题1:解:(1)设抛物线的解析式为: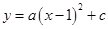 , ,
把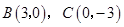 代入得: 代入得: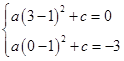 解得 解得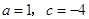
 抛物线的解析式为 抛物线的解析式为 ,即 ,即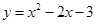
小题2:(2)存在.  由对称性可知, 由对称性可知,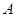 点的坐标为 点的坐标为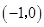
 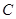 点坐标为 点坐标为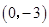 ,B点坐标为(3,0), ,B点坐标为(3,0),
 直线BC的解析式为 直线BC的解析式为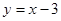
 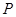 点在对称轴上,设 点在对称轴上,设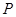 点坐标为 点坐标为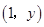 代入 代入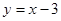 ,求得 ,求得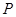 点坐标为(1,-2) 点坐标为(1,-2)
小题3:(3)证明:设圆的半径为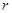 ,依题意有 ,依题意有
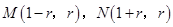 把 把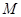 的坐标代入 的坐标代入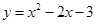 , 整理 , 整理
得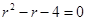 , 解得 , 解得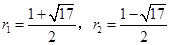 (舍去) (舍去)
 所求圆的直径为 所求圆的直径为 . . |
据专家权威分析,试题“(本题满分12分)在平面直角坐标系中,抛物线交轴于两点,交轴于点..”主要考查你对 二次函数的定义,二次函数的图像,二次函数的最大值和最小值,求二次函数的解析式及二次函数的应用 等考点的理解。关于这些考点的“档案”如下:
二次函数的定义二次函数的图像二次函数的最大值和最小值求二次函数的解析式及二次函数的应用
考点名称:二次函数的定义 考点名称:二次函数的图像 考点名称:二次函数的最大值和最小值 考点名称:求二次函数的解析式及二次函数的应用
|

