| 已知如图,对称轴为直线的抛物线与轴相交于点B、O.(1)求抛物线的解析式,并求出顶点A的坐标.(2)连结AB,平移AB所在的直线,使其经过原点O,得到直线.点是上一动点,当△的周-九年级数学 |
|
[db:作者] 2019-05-21 00:00:00 零零社区 |
|
|
题文
已知如图,对称轴为直线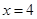 的抛物线 的抛物线 与 与 轴相交于点B、O. 轴相交于点B、O.
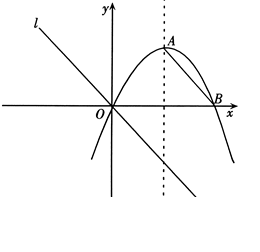
(1)求抛物线的解析式,并求出顶点A的坐标.
(2) 连结AB,平移AB所在的直线,使其经过原点O,得到直线 .点 .点 是 是 上一动点,当△ 上一动点,当△ 的周长最小时,求点P的坐标. 的周长最小时,求点P的坐标.
(3)当△ 的周长最小时,在直线AB的上方是否存在一点Q,使以A,B,Q为顶点的三角形与△POB相似,若存在,直接写出点Q的坐标;若不存在,说明理由.(规定:点Q的对应顶点不为点O) 的周长最小时,在直线AB的上方是否存在一点Q,使以A,B,Q为顶点的三角形与△POB相似,若存在,直接写出点Q的坐标;若不存在,说明理由.(规定:点Q的对应顶点不为点O) |
题型:解答题 难度:中档
答案
(1) ,(4,4)(2) (2,-2)(3)存在,点 ,(4,4)(2) (2,-2)(3)存在,点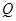 坐标为(8,16)、(20,4)(8,2)、(6,4) 坐标为(8,16)、(20,4)(8,2)、(6,4) |
(1)∵点B与O(0,0)关于直线x=4对称,
∴点B坐标为(8,0).
将点B坐标代入 得: 得:
64 +16=0, +16=0,
∴ = = . .
∴抛物线解析式为 . 2分 . 2分
当 =4时, =4时, , ,
∴顶点A坐标为(4,4). 2分
(说明:可用对称轴为 ,求 ,求 值,用顶点式求顶点A坐标.) 值,用顶点式求顶点A坐标.)
(2)设直线AB解析式为y=kx+b.
∵A(4,4),B(8,0),
∴ 解得 , ∴ , ∴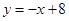 .- .-
∵直线 ∥AB且过点O, ∥AB且过点O,
∴直线 解析式为 解析式为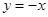 . .
A关于直线 的对称点是A1(-4,-4),连接A1B,则直线A1B的函数关系式是 的对称点是A1(-4,-4),连接A1B,则直线A1B的函数关系式是

由 得交点P(2,-2) 4分 得交点P(2,-2) 4分
(3)存在,点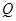 坐标为(8,16)、(20,4)(8,2)、(6,4) 4分 坐标为(8,16)、(20,4)(8,2)、(6,4) 4分
主要考查了一次函数、二次函数解析式的确定,函数图象交点及图形面积的求法等重要知识点,同时还考查了分类讨论的数学思想,难度较大 |
据专家权威分析,试题“已知如图,对称轴为直线的抛物线与轴相交于点B、O.(1)求抛物线的..”主要考查你对 二次函数的定义,二次函数的图像,二次函数的最大值和最小值,求二次函数的解析式及二次函数的应用 等考点的理解。关于这些考点的“档案”如下:
二次函数的定义二次函数的图像二次函数的最大值和最小值求二次函数的解析式及二次函数的应用
考点名称:二次函数的定义 考点名称:二次函数的图像 考点名称:二次函数的最大值和最小值 考点名称:求二次函数的解析式及二次函数的应用
|
|
http://www.00-edu.com/ks/shuxue/2/117/2019-05-21/1142699.html十二生肖十二星座
|

