|
题文
如图,抛物线 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C. 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
(1)求点A、B的坐标;
(2)设D为已知抛物线的对称轴上的任意一点,当△ACD的面积等于△ACB的面积时,求点D的坐标;
(3)若直线l过点E(4,0),M为直线l上的动点,当以A、B、M为顶点所作的直角三角形有且只有三个时,求直线l的解析式. |
题型:解答题 难度:偏易
答案
解:(1)在 中,令y=0,即 中,令y=0,即 ,解得x1=﹣4,x2=2。 ,解得x1=﹣4,x2=2。
∵点A在点B的左侧,∴A、B点的坐标为A(﹣4,0)、B(2,0)。
(2)由 得,对称轴为x=﹣1。 得,对称轴为x=﹣1。
在 中,令x=0,得y=3。 中,令x=0,得y=3。
∴OC=3,AB=6, 。 。
在Rt△AOC中, 。 。
设△ACD中AC边上的高为h,则有 AC?h=9,解得h= AC?h=9,解得h= 。 。
如图1,在坐标平面内作直线平行于AC,且到AC的距离=h= ,这样的直线有2条,分别是L1和L2,则直线与对称轴x=﹣1的两个交点即为所求的点D。 ,这样的直线有2条,分别是L1和L2,则直线与对称轴x=﹣1的两个交点即为所求的点D。

设L1交y轴于E,过C作CF⊥L1于F,则CF=h= , ,
∴ 。 。
设直线AC的解析式为y=kx+b,
将A(﹣4,0),B(0,3)坐标代入,得
 ,解得 ,解得 。 。
∴直线AC解析式为 。 。
直线L1可以看做直线AC向下平移CE长度单位(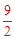 个长度单位)而形成的, 个长度单位)而形成的,
∴直线L1的解析式为 。 。
则D1的纵坐标为 。∴D1(﹣4, 。∴D1(﹣4, )。 )。
同理,直线AC向上平移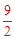 个长度单位得到L2,可求得D2(﹣1, 个长度单位得到L2,可求得D2(﹣1,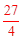 )。 )。
综上所述,D点坐标为:D1(﹣4, ),D2(﹣1, ),D2(﹣1,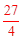 )。 )。
(3)如图2,以AB为直径作⊙F,圆心为F.过E点作⊙F的切线,这样的切线有2条.
连接FM,过M作MN⊥x轴于点N。
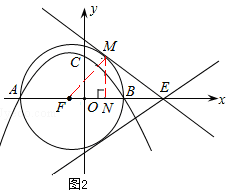
∵A(﹣4,0),B(2,0),∴F(﹣1,0),⊙F半径FM=FB=3。
又FE=5,则在Rt△MEF中,-
ME=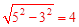 ,sin∠MFE= ,sin∠MFE= ,cos∠MFE= ,cos∠MFE=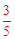 。 。
在Rt△FMN中,MN=MN?sin∠MFE=3× , ,
FN=MN?cos∠MFE=3×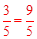 。 。
则ON= 。∴M点坐标为( 。∴M点坐标为( , , )。 )。
直线l过M( , , ),E(4,0), ),E(4,0),
设直线l的解析式为y=k1x+b1,则有 ,解得 ,解得 。 。
∴直线l的解析式为y= x+3。 x+3。
同理,可以求得另一条切线的解析式为y= x﹣3。 x﹣3。
综上所述,直线l的解析式为y= x+3或y= x+3或y= x﹣3。 x﹣3。 |
二次函数综合题,待定系数法,曲线上点的坐标与方程的关系,二次函数的性质,勾股定理,直线平行和平移的性质,直线与圆的位置关系,直线与圆相切的性质,圆周角定理,锐角三角函数定义。
(1)A、B点为抛物线与x轴交点,令y=0,解一元二次方程即可求解。
(2)根据题意求出△ACD中AC边上的高,设为h.在坐标平面内,作AC的平行线,平行线之间的距离等于h.根据等底等高面积相等的原理,则平行线与坐标轴的交点即为所求的D点.从一次函数的观点来看,这样的平行线可以看做是直线AC向上或向下平移而形成.因此先求出直线AC的解析式,再求出平移距离,即可求得所作平行线的解析式,从而求得D点坐标。这样的平行线有两条。
(3)本问关键是理解“以A、B、M为顶点所作的直角三角形有且只有三个”的含义.因为过A、B点作x轴的垂线,其与直线l的两个交点均可以与A、B点构成直角三角形,这样已经有符合题意的两个直角三角形;第三个直角三角形从直线与圆的位置关系方面考虑,以AB为直径作圆,当直线与圆相切时,根据圆周角定理,切点与A、B点构成直角三角形.从而问题得解。这样的切线有两条。 |
据专家权威分析,试题“如图,抛物线与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C...”主要考查你对 二次函数的定义,二次函数的图像,二次函数的最大值和最小值,求二次函数的解析式及二次函数的应用 等考点的理解。关于这些考点的“档案”如下:
二次函数的定义二次函数的图像二次函数的最大值和最小值求二次函数的解析式及二次函数的应用
考点名称:二次函数的定义 考点名称:二次函数的图像 考点名称:二次函数的最大值和最小值 考点名称:求二次函数的解析式及二次函数的应用
|

