|
题文
已知抛物线y=ax2+bx+c ,当x=0时,有最小值为1 ;且在直线y=2上截得的线段长为4 .

(1)求此抛物线的解析式;
(2)若点P是抛物线的任意一点,记点P到X轴的距离为d1,点P 与点 F (0,2)的距离为d 2 ,猜想d1、 d 2的大小关系,并证明;
(3)若直线PF交此抛物线于另一点Q(异于P点)。 试判断以PQ为直径的圆与x 轴的位置关系,并说明理由。 |
题型:解答题 难度:中档
答案
(1)求此抛物线的解析式: y=
(2)猜想:d1 =" d" 2 .
设d的坐标为(x, 0.25x2+1)
d1=
 = |0.25x2+1 | = |0.25x2+1 |
∴d1=
(3) 以PQ为直径的圆与x 轴相切
设Q到x轴的距离为m,到F的距离为n,
根据(2)的结论,有m=n,
过PQ的中点作x的垂线,设其长度为h,
易得h=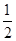 (m+d1), (m+d1),
同时有PQ=(n+d2)=(m+d1),
为h的2倍,
故以PQ为直径的圆与x轴相切. |
(1)由x=0时,有最小值为1得(0,1)点经过抛物线,由在直线y=2上截得的线段长为4得出(2,2)、(-2,2)点经过抛物线,把这三点代入求出抛物线的解析式;
(2)由勾股定理即可d1 = ; ;
(3)由(2)的结论,找PQ的中点到x轴的距离与PQ的大小关系,容易证得两者相等;故以PQ为直径的圆与x轴相切. |
据专家权威分析,试题“已知抛物线y=ax2+bx+c,当x=0时,有最小值为1;且在直线y=2上截得..”主要考查你对 二次函数的定义,二次函数的图像,二次函数的最大值和最小值,求二次函数的解析式及二次函数的应用 等考点的理解。关于这些考点的“档案”如下:
二次函数的定义二次函数的图像二次函数的最大值和最小值求二次函数的解析式及二次函数的应用
考点名称:二次函数的定义 考点名称:二次函数的图像 考点名称:二次函数的最大值和最小值 考点名称:求二次函数的解析式及二次函数的应用
|

