|
题文
已知二次函数 : :
(1) 证明:当m为整数时,抛物线 与x轴交点的横坐标均为整数; 与x轴交点的横坐标均为整数;
(2) 以抛物线 的顶点A为等腰Rt△的直角顶点,作该抛物线的内接等腰Rt△ABC(B、C两点在抛物线上),求Rt△ABC的面积(图中给出的是m取某一值时的示意图); 的顶点A为等腰Rt△的直角顶点,作该抛物线的内接等腰Rt△ABC(B、C两点在抛物线上),求Rt△ABC的面积(图中给出的是m取某一值时的示意图);
(3) 若抛物线 与直线y=7交点的横坐标均为整数,求整数m的值. 与直线y=7交点的横坐标均为整数,求整数m的值. |
题型:解答题 难度:中档
答案
(1)证明:令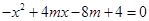 ,解得抛物线与 ,解得抛物线与 轴交点的横坐标x, 轴交点的横坐标x,
 , ,
∵m是整数,∴ 是整数,∴ 是整数,∴ 均为整数 均为整数
(2) 求得顶点A(2m,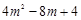 ),根据抛物线的轴对称性,所以BC平行x轴, ),根据抛物线的轴对称性,所以BC平行x轴,
作AD⊥BC,设B(a,b),则D在对称轴上,D(2m,b),
则BD=2m-a,(2m>a),
AD=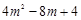 -b -b
=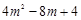  =(2m-a)2 =(2m-a)2
∵AD=BD, ∴(2m-a)2=(2m-a), 解得2m-a=1或2m-a=0(舍去)
∴S△ABC= BCAD= BCAD= ×2BD×AD=1 ×2BD×AD=1

(3)由 , , , ,
当x为整数时,须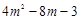 为完全平方数,设 为完全平方数,设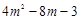  (n是整数)整理得: (n是整数)整理得: 即 即
两个整数的积为7,∴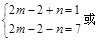 ~ ~ ~ ~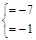 ~ ~
解得:    综上得: m=3或m=-1 综上得: m=3或m=-1
∴抛物线与直线y=7交点的横坐标均为整数时,m=3或m=-1. |
(1)表示出横坐标,然后分析是整数;
(2)得出BC平行x轴、D在对称轴上是求三角形面积的关键;
(3)当x为整数时,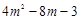 为完全平方数,然后根据两个整数的积=7求解。 为完全平方数,然后根据两个整数的积=7求解。 |
据专家权威分析,试题“已知二次函数:(1)证明:当m为整数时,抛物线与x轴交点的横坐标均为..”主要考查你对 二次函数的定义,二次函数的图像,二次函数的最大值和最小值,求二次函数的解析式及二次函数的应用 等考点的理解。关于这些考点的“档案”如下:
二次函数的定义二次函数的图像二次函数的最大值和最小值求二次函数的解析式及二次函数的应用
考点名称:二次函数的定义 考点名称:二次函数的图像 考点名称:二次函数的最大值和最小值 考点名称:求二次函数的解析式及二次函数的应用
|

