如图，在平面直角坐标系中，已知抛物线经过点Ａ(0，4)，B(1，0)，C（5，0），抛物线对称轴与轴相交于点M．（1）求抛物线的解析式和对称轴；（2）设点P为抛物线（）上的一点，若以A、O、-九年级数学打印页面

如图，在平面直角坐标系中，已知抛物线经过点Ａ(0，4)，B(1，0)，C（5，0），抛物线对称轴与轴相交于点M．（1）求抛物线的解析式和对称轴；（2）设点P为抛物线（）上的一点，若以A、O、-九年级数学

[db:作者] 2019-05-21 00:00:00 互联网

题文

如图，在平面直角坐标系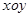中，已知抛物线经过点Ａ(0，4)，B(1，0)，C（5，0），抛物线对称轴与轴相交于点M．
（1）求抛物线的解析式和对称轴；
（2）设点P为抛物线（）上的一点，若以A、O、M、P为顶点的四边形四条边的长度为四个连续的
正整数，请你直接写出点P的坐标；
（3）连接AC．探索：在直线AC下方的抛物线上是否存在一点N，使△NAC的面积最大？若存在，请你求
出点N的坐标；若不存在，请你说明理由．
题型：解答题  难度：中档

答案

（1）根据已知条件可设抛物线的解析式为，
　　把点A（0，4）代入上式得：，
　　∴，
　　∴抛物线的对称轴是：．
（2）由已知，可求得P（6，4）．

提示：由题意可知以A、O、M、P为顶点的四边形有两条边AO=4、OM=3，又知点P的坐标中，所以，MP>2,AP>2；因此以1、2、3、4为边或以2、3、4、5为边都不符合题意，所以四条边的长只能是3、4、5、6的一种情况，在Rt△AOM中，，因为抛物线对称轴过点M，所以在抛物线的图象上有关于点A的对称点与M的距离为5，即PM=5，此时点P横坐标为6，即AP=6；故以A、O、M、P为顶点的四边形的四条边长度分别是四个连续的正整数3、4、5、6成立，
即P（6，4）．
⑶法一：在直线AC的下方的抛物线上存在点N，使△NAC面积最大．

设N点的横坐标为，此时点N（，过点N作NG∥轴交AC于G；由点A（0，4）和点C（5，0）可求出直线AC的解析式为：；把代入得：，则G，
此时：NG=-（），
=．
∴
∴当时，△CAN面积的最大值为，
由，得：，∴N（， -3）．
法二：提示：过点N作轴的平行线交轴于点E，作CF⊥EN于点F，则
（1）抛物线经过点A（0，4），B（1，0），C（5，0），可利用两点式法设抛物线的解析式为y=a（x-1）（x-5），代入A（0，4）即可求得函数的解析式，则可求得抛物线的对称轴；
（2）由已知，可求得P（6，4），由题意可知以A、O、M、P为顶点的四边形有两条边AO=4、OM=3，又知点P的坐标中x＞5，所以MP＞2，AP＞2；因此以1、2、3、4为边或以2、3、4、5为边都不符合题意，所以四条边的长只能是3、4、5、6的一种情况，则分析求解即可求得答案；
（3）在直线AC的下方的抛物线上存在点N，使△NAC面积最大．设N点的横坐标为t，此时点N（t，）（0＜t＜5），再求得直线AC的解析式，即可求得NG的长与△ACN的面积，由二次函数最大值的问题即可求得答案．

据专家权威分析，试题“如图，在平面直角坐标系中，已知抛物线经过点Ａ(0，4)，B(1，0)，..”主要考查你对二次函数的定义，二次函数的图像，二次函数的最大值和最小值，求二次函数的解析式及二次函数的应用等考点的理解。关于这些考点的“档案”如下：

二次函数的定义二次函数的图像二次函数的最大值和最小值求二次函数的解析式及二次函数的应用

考点名称：二次函数的定义

定义：
一般地，如果（a，b，c是常数，a≠0），那么y叫做x 的二次函数。
①所谓二次函数就是说自变量最高次数是2;
②二次函数（a≠0）中x、y是变量，a，b，c是常数，自变量x 的取值范围是全体实数，b和c可以是任意实数，a是不等于0的实数，因为a=0时，变为y=bx+c若b≠0,则y=bx+c是一次函数，若b=0，则y=c是一个常数函数。
③二次函数（a≠0）与一元二次方程（a≠0）有密切联系，如果将变量y换成一个常数，那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式：
（1）一般式：（a，b，c是常数，a≠0）；
（2）顶点式：（a，h，k是常数，a≠0）
（3）当抛物线与x轴有交点时，即对应二次好方程有实根x₁和x₂存在时，根据二次三项式的分解因式，二次函数可转化为两根式。如果没有交点，则不能这样表示。

二次函数的一般形式的结构特征：
①函数的关系式是整式；
②自变量的最高次数是2；
③二次项系数不等于零。
二次函数的判定：
二次函数的一般形式中等号右边是关于自变量x的二次三项式；
当b=0，c=0时，y=ax²是特殊的二次函数；
判断一个函数是不是二次函数，在关系式是整式的前提下，如果把关系式化简整理（去括号、合并同类项）后，能写成（a≠0）的形式，那么这个函数就是二次函数，否则就不是。

考点名称：二次函数的图像

二次函数的图像
是一条关于对称的曲线，这条曲线叫抛物线。
抛物线的主要特征：
①有开口方向，a表示开口方向：a>0时，抛物线开口向上；a<0时，抛物线开口向下；
②有对称轴；
③有顶点；
④c 表示抛物线与y轴的交点坐标：（0，c）。
二次函数图像性质：
轴对称：
二次函数图像是轴对称图形。对称轴为直线x=-b/2a
对称轴与二次函数图像唯一的交点为二次函数图像的顶点P。
特别地，当b=0时，二次函数图像的对称轴是y轴（即直线x=0）。
a,b同号，对称轴在y轴左侧
b=0,对称轴是y轴
a,b异号，对称轴在y轴右侧

顶点：
二次函数图像有一个顶点P，坐标为P ( h,k )
当h=0时，P在y轴上；当k=0时，P在x轴上。即可表示为顶点式y=a(x-h)^2+k。
h=-b/2a， k=(4ac-b^2)/4a。

开口：
二次项系数a决定二次函数图像的开口方向和大小。
当a>0时，二次函数图像向上开口；当a<0时，抛物线向下开口。
|a|越大，则二次函数图像的开口越小。
决定对称轴位置的因素：
一次项系数b和二次项系数a共同决定对称轴的位置。
当a>0,与b同号时（即ab>0），对称轴在y轴左；因为对称轴在左边则对称轴小于0，也就是- b/2a<0,所以 b/2a要大于0，所以a、b要同号
当a>0,与b异号时（即ab<0），对称轴在y轴右。因为对称轴在右边则对称轴要大于0，也就是- b/2a>0, 所以b/2a要小于0，所以a、b要异号
可简单记忆为左同右异，即当a与b同号时（即ab>0），对称轴在y轴左；当a与b异号时（即ab<0 ），对称轴在y轴右。
事实上，b有其自身的几何意义：二次函数图像与y轴的交点处的该二次函数图像切线的函数解析式（一次函数）的斜率k的值。可通过对二次函数求导得到。

决定与y轴交点的因素:
常数项c决定二次函数图像与y轴交点。
二次函数图像与y轴交于（0,C）
注意：顶点坐标为（h,k)，与y轴交于（0,C)。

与x轴交点个数：
a<0;k>0或a>0;k<0时，二次函数图像与x轴有2个交点。
k=0时，二次函数图像与x轴只有1个交点。
a<0;k<0或a>0,k>0时，二次函数图像与X轴无交点。
当a>0时，函数在x=h处取得最小值ymin=k，在x<h范围内是减函数，在x>h范围内是增函数（即y随x的变大而变小），二次函数图像的开口向上，函数的值域是y>k
当a<0时，函数在x=h处取得最大值ymax=k，在x<h范围内是增函数，在x>h范围内是减函数（即y随x的变大而变大），二次函数图像的开口向下，函数的值域是y<k
当h=0时，抛物线的对称轴是y轴，这时，函数是偶函数。

考点名称：二次函数的最大值和最小值

二次函数的最值：
1.如果自变量的取值范围是全体实数，则当a>0时，抛物线开口向上，有最低点，那么函数在处取得最小值y_最小值=；
当a<0时，抛物线开口向下，有最高点，即当时，函数取得最大值，y_最大值=。
也即是：如果自变量的取值范围是全体实数，那么函数在顶点处取得最大值（或最小值），即当时，。
2.如果自变量的取值范围是，那么，首先要看是否在自变量取值范围内，若在此范围内，则当x=时，；若不在此范围内，则需要考虑函数在范围内的增减性，如果在此范围内，y随x的增大而增大，则当x=x₂ 时，，当x=x₁ 时；如果在此范围内，y随x的增大而减小，则当x=x₁时，，当x=x₂时。

考点名称：求二次函数的解析式及二次函数的应用

求二次函数的解析式：
最常用的方法是待定系数法，根据题目的特点，选择恰当的形式，一般，有如下几种情况：
（1）已知抛物线上三点的坐标，一般选用一般式；
（2）已知抛物线顶点或对称轴或最大（小）值，一般选用顶点式；
（3）已知抛物线与x轴的两个交点的横坐标，一般选用两点式；
（4）已知抛物线上纵坐标相同的两点，常选用顶点式。

二次函数的应用：
（1）应用二次函数才解决实际问题的一般思路：
理解题意；
建立数学模型；
解决题目提出的问题。
（2）应用二次函数求实际问题中的最值：
即解二次函数最值应用题，设法把关于最值的实际问题转化为二次函数的最值问题，然后按求二次函数最值的方法求解。
求最值时，要注意求得答案要符合实际问题。
二次函数的三种表达形式：
①一般式：
y=ax2+bx+c(a≠0,a、b、c为常数)，顶点坐标为 [,]
把三个点代入函数解析式得出一个三元一次方程组，就能解出a、b、c的值。

②顶点式：
y=a(x-h)2+k(a≠0,a、h、k为常数),顶点坐标为对称轴为直线x=h，顶点的位置特征和图像的开口方向与函数y=ax²的图像相同，当x=h时，y最值=k。
有时题目会指出让你用配方法把一般式化成顶点式。
例：已知二次函数y的顶点(1,2)和另一任意点(3,10)，求y的解析式。
解：设y=a(x-1)2+2，把(3,10)代入上式，解得y=2(x-1)2+2。
注意：与点在平面直角坐标系中的平移不同，二次函数平移后的顶点式中，h>0时，h越大，图像的对称轴离y轴越远，且在x轴正方向上，不能因h前是负号就简单地认为是向左平移。
具体可分为下面几种情况：
当h>0时，y=a(x-h)2的图象可由抛物线y=ax2向右平行移动h个单位得到；
当h<0时，y=a(x-h)2的图象可由抛物线y=ax2向左平行移动|h|个单位得到；
当h>0,k>0时，将抛物线y=ax2向右平行移动h个单位，再向上移动k个单位，就可以得到y=a(x-h)2+k的图象；
当h>0,k<0时，将抛物线y=ax2向右平行移动h个单位，再向下移动|k|个单位可得到y=a(x-h)2+k的图象；
当h<0,k>0时，将抛物线y=ax2向左平行移动|h|个单位，再向上移动k个单位可得到y=a(x-h)2+k的图象；
当h<0,k<0时，将抛物线y=ax2向左平行移动|h|个单位，再向下移动|k|个单位可得到y=a(x-h)2+k的图象。

③交点式：
y=a(x-x₁)(x-x₂) (a≠0) [仅限于与x轴即y=0有交点时的抛物线，即b²-4ac≥0] .
已知抛物线与x轴即y=0有交点A（x₁，0）和 B（x₂，0）,我们可设y=a(x-x₁)(x-x₂),然后把第三点代入x、y中便可求出a。

由一般式变为交点式的步骤：
二次函数
∵x₁+x₂=-b/a， x₁?x₂=c/a(由韦达定理得),
∴y=ax2+bx+c
=a(x2+b/ax+c/a)
=a[x2-(x₁+x₂)x+x₁?x₂]
=a(x-x₁)(x-x₂).
重要概念：
a，b，c为常数，a≠0，且a决定函数的开口方向。a>0时，开口方向向上；
a<0时，开口方向向下。a的绝对值可以决定开口大小。
a的绝对值越大开口就越小，a的绝对值越小开口就越大。
能灵活运用这三种方式求二次函数的解析式；
能熟练地运用二次函数在几何领域中的应用；
能熟练地运用二次函数解决实际问题。
二次函数的其他表达形式：
①牛顿插值公式:
f(x)=f[x₀]+f[x₀,x₁](x-x₀)+f[x₀,x₁,x₂](x-x₀)(x-x₁)+...f[x₀,...x_n](x-x₀)...(x-_xn-1)+Rn(x)由此可引导出交点式的系数a=y/(x·x)(y为截距)　
二次函数表达式的右边通常为二次三项式。

双根式
y=a(x-x₁)*(x-x2)
若ax2+bx+c=0有两个实根x₁,x₂，则y=a(x-x₁)(x-x₂)此抛物线的对称轴为直线x=(x₁+x₂)/2。

③三点式
已知二次函数上三个点，（x₁,f(x₁)）（x₂,f(x₂)）（x₃,f(x₃)）
则f(x)=f(x₃)(x-x₁)(x-x₂)/(x₃-x₁)(x₃-x₂)+f(x₂)(x-x₁)*(x-x₃)/(x₂-x₁)(x₂-x₃)+f(x₁)(x-x₂)(x-x₃)/(x₁-x₂)(x₁-x₃)
与X轴交点的情况
当△=b2-4ac>0时，函数图像与x轴有两个交点。(x₁,0), (x₂,0);
当△=b2-4ac=0时，函数图像与x轴只有一个交点。(-b/2a，0)。
Δ=b2-4ac<0时，抛物线与x轴没有交点。
X的取值是虚数（x=-b±√b2－4ac的值的相反数，乘上虚数i，整个式子除以2a）
二次函数解释式的求法：
就一般式y=ax2＋bx＋c（其中a，b，c为常数，且a≠0）而言，其中含有三个待定的系数a ，b ，c．求二次函数的一般式时，必须要有三个独立的定量条件，来建立关于a ，b ，c 的方程，联立求解，再把求出的a ，b ，c 的值反代回原函数解析式，即可得到所求的二次函数解析式。

1.巧取交点式法：
知识归纳：二次函数交点式：y＝a(x－x₁)(x－x₂) （a≠0）x₁，x₂分别是抛物线与x轴两个交点的横坐标。
已知抛物线与x轴两个交点的横坐标求二次函数解析式时，用交点式比较简便。
①典型例题一：告诉抛物线与x轴的两个交点的横坐标，和第三个点，可求出函数的交点式。
例：已知抛物线与x轴交点的横坐标为-2和1 ，且通过点（2，8），求二次函数的解析式。
点拨：
解设函数的解析式为y＝a(x+2)(x-1)，
∵过点（2，8），
∴8＝a(2+2)(2-1)。
解得a=2，
∴抛物线的解析式为：
y＝2(x+2)(x-1)，
即y＝2x2+2x-4。

②典型例题二：告诉抛物线与x轴的两个交点之间的距离和对称轴，可利用抛物线的对称性求解。
例：已知二次函数的顶点坐标为（3，-2），并且图象与x轴两交点间的距离为4，求二次函数的解析式。
点拨：
在已知抛物线与x轴两交点的距离和顶点坐标的情况下，问题比较容易解决．由顶点坐标为（3，-2）的条件，易知其对称轴为x＝3，再利用抛物线的对称性，可知图象与x轴两交点的坐标分别为（1，0）和（5，0）。此时，可使用二次函数的交点式，得出函数解析式。

2.巧用顶点式：
顶点式y=a(x－h)²+k（a≠0），其中（h，k）是抛物线的顶点。当已知抛物线顶点坐标或对称轴，或能够先求出抛物线顶点时，设顶点式解题十分简洁，因为其中只有一个未知数a。在此类问题中，常和对称轴，最大值或最小值结合起来命题。在应用题中，涉及到桥拱、隧道、弹道曲线、投篮等问题时，一般用顶点式方便．
①典型例题一：告诉顶点坐标和另一个点的坐标，直接可以解出函数顶点式。
例：已知抛物线的顶点坐标为（-1，-2），且通过点（1，10），求此二次函数的解析式。
点拨：
解∵顶点坐标为（-1，-2），
故设二次函数解析式为y=a(x+1)²-2 （a≠0）。
把点（1，10）代入上式，得10=a·(1+1)²-2。
∴a=3。
∴二次函数的解析式为y=3(x+1)²-2，即y=3x²+6x+1。

②典型例题二：
如果a>0，那么当时，y有最小值且y_最小=；
如果a<0，那么，当时，y有最大值，且y_最大=。
告诉最大值或最小值，实际上也是告诉了顶点坐标，同样也可以求出顶点式。
例：已知二次函数当x＝4时有最小值－3，且它的图象与x轴两交点间的距离为6，求这个二次函数的解析式。
点拨：
析解∵二次函数当x＝4时有最小值－3，∴顶点坐标为（4，-3），对称轴为直线x＝4，抛物线开口向上。
由于图象与x轴两交点间的距离为6，根据图象的对称性就可以得到图象与x轴两交点的坐标是（1，0）和（7，0）。
∴抛物线的顶点为（4，-3）且过点（1，0）。
故可设函数解析式为y＝a(x－4)²－3。
将（1，0）代入得0＝a(1－4)²－3, 解得a＝13．
∴y＝13(x－4)²-3，即y＝13x²－83x＋73。
③典型例题三：告诉对称轴，相当于告诉了顶点的横坐标，综合其他条件，也可解出。
例如：
（1）已知二次函数的图象经过点A（3，-2）和B（1，0），且对称轴是直线x＝3．求这个二次函数的解析式.
（2）已知关于x的二次函数图象的对称轴是直线x=1，图象交y轴于点（0，2），且过点（-1，0），求这个二次函数的解析式.
（3）已知抛物线的对称轴为直线x=2，且通过点（1，4）和点（5，0），求此抛物线的解析式.
（4）二次函数的图象的对称轴x=-4，且过原点，它的顶点到x轴的距离为4，求此函数的解析式．

④典型例题四：利用函数的顶点式，解图像的平移等问题非常方便。
例：把抛物线y=ax2+bx+c的图像向右平移3 个单位, 再向下平移2 个单位, 所得图像的解析式是y=x2-3x+5, 则函数的解析式为_______。
点拨：
解先将y=x2-3x+5化为y=(x-32)2+5-94, 即y=(x-32)2+114。
∵它是由抛物线的图像向右平移3 个单位, 再向下平移2 个单位得到的，
∴原抛物线的解析式是y=(x-32+3)2+114+2=(x+32)2+194=x2+3x+7。

http://www.00-edu.com/ks/shuxue/2/117/2019-05-21/1142799.html十二生肖
十二星座