|
题文
阅读材料,并解答问题。
我们已经学过了一元一次不等式的解法,对于一些特殊的不等式,我们用作函数图象的方法求出它的解集,这也是《数学新课程标准》中所要求掌物的内容。例如:如何求不等式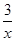 ﹥x+2的解集呢? 我们可以设 ﹥x+2的解集呢? 我们可以设 = =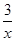 , , =x+2.然后求出它们的交点的坐标, 并在同一直角坐标系中画出它们的函数图象,通过看图,可以发现此不等式的解集是“xく-3或0くxく1” 用上面的知识解决问题:求不等式x =x+2.然后求出它们的交点的坐标, 并在同一直角坐标系中画出它们的函数图象,通过看图,可以发现此不等式的解集是“xく-3或0くxく1” 用上面的知识解决问题:求不等式x -x>x+3的解集. -x>x+3的解集.
(1)设函数 = , = ,  = =
(2)两个函数图象的交点坐标为
(3)在所给的直角坐标系中画出两个函数的图象(不要列表).
(4)观察发现:不等式x -x>x+3的解集为 -x>x+3的解集为  |
题型:解答题 难度:中档
答案
(1)y1=x2-x,y2=x+3(2)(-1,2),(3,6)(3) (4)x>3或x<-1 (4)x>3或x<-1 |
(1)由题意,设y1=x2-x,y2=x+3;
(2)解方程:x2-x=x+3,
得:x1=-1,x2=3,
当x=-1时,y1=2;当x=3时,y1=6,
即两个函数的交点坐标分别为:(-1,2),(3,6);
(3)如图:
(4)从图象得到:当x>3或x<-1时,一次函数的图象在抛物线的下方,
∴不等式x2-x>x+3的解集为:x>3或x<-1.
根据阅读材料可以得到,把不等式的问题转化为两个函数的问题,根据图象解题. |
据专家权威分析,试题“阅读材料,并解答问题。我们已经学过了一元一次不等式的解法,对..”主要考查你对 二次函数的定义,二次函数的图像,二次函数的最大值和最小值,求二次函数的解析式及二次函数的应用 等考点的理解。关于这些考点的“档案”如下:
二次函数的定义二次函数的图像二次函数的最大值和最小值求二次函数的解析式及二次函数的应用
考点名称:二次函数的定义 考点名称:二次函数的图像 考点名称:二次函数的最大值和最小值 考点名称:求二次函数的解析式及二次函数的应用
|

