|
题文
如图,在平面直角坐标系 中,把抛物线 中,把抛物线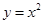 向左平移1个单位,再向下平移4个单位,得到抛物线 向左平移1个单位,再向下平移4个单位,得到抛物线 .所得抛物线与 .所得抛物线与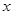 轴交于 轴交于 两点(点 两点(点 在点 在点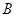 的左边),与 的左边),与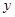 轴交于点 轴交于点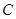 ,顶点为 ,顶点为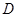 . .

(1)写出 的值; 的值;
(2)判断 的形状,并说明理由; 的形状,并说明理由;
(3)在线段 上是否存在点 上是否存在点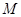 ,使 ,使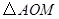 ∽ ∽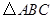 ?若存在,求出点 ?若存在,求出点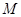 的坐标;若不存在,说明理由. 的坐标;若不存在,说明理由. |
题型:解答题 难度:中档
答案
(1)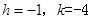 (2)直角三角形,理由见解析(3)存在, (2)直角三角形,理由见解析(3)存在, |
解:(1)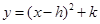 的顶点坐标为D(-1,-4), 的顶点坐标为D(-1,-4),
∴ 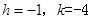 . …………………………………………2分 . …………………………………………2分
(2)由(1)得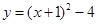 . .
当 时, 时, . 解之,得 . 解之,得  . .
∴  . .
又当 时, 时, , ,
∴C点坐标为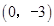 .………………………………4分 .………………………………4分
又抛物线顶点坐标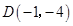 ,作抛物线的对称轴 ,作抛物线的对称轴 交 交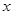 轴于点E, 轴于点E, 轴于点 轴于点 .易知 .易知
在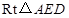 中, 中, ; ;
在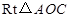 中, 中, ; ;
在 中, 中, ; ;
∴ 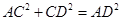 . .
∴ △ACD是直角三角形.…………………………6分
(2)存在.作OM∥BC交AC于M,M点即为所求点.

由(2)知, 为等腰直角三角形, 为等腰直角三角形, , , . .
由 ,得 ,得 . .
即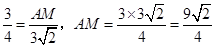 . …………………………9分 . …………………………9分
过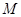 点作 点作 于点 于点 ,则 ,则
 , , . .
又点M在第三象限,所以 . …………………………12分 . …………………………12分
(1)由抛物线的顶点坐标特征可以求得 的值; 的值;
(2)先由抛物线函数关系式求得点A、C、D的坐标,再根据勾股定理可以求出AC、AD、CD的长,因为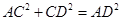 ,所以△ACD是直角三角形. ,所以△ACD是直角三角形.
(3)由 ,根据对应边成比例可求出AM的长,过 ,根据对应边成比例可求出AM的长,过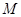 点作 点作 于点 于点 ,根据勾股定理可求出AG、MG的长,再求得OG的长,从而得到点 ,根据勾股定理可求出AG、MG的长,再求得OG的长,从而得到点 的坐标。 的坐标。 |
据专家权威分析,试题“如图,在平面直角坐标系中,把抛物线向左平移1个单位,再向下平移..”主要考查你对 二次函数的定义,二次函数的图像,二次函数的最大值和最小值,求二次函数的解析式及二次函数的应用 等考点的理解。关于这些考点的“档案”如下:
二次函数的定义二次函数的图像二次函数的最大值和最小值求二次函数的解析式及二次函数的应用
考点名称:二次函数的定义 考点名称:二次函数的图像 考点名称:二次函数的最大值和最小值 考点名称:求二次函数的解析式及二次函数的应用
|

