|
题文
如图14,已知点A(-1,0),B(4,0),点C在y轴的正半轴上,且∠ACB=900,抛物线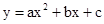 经过A、B、C三点,其顶点为M. 经过A、B、C三点,其顶点为M.
求抛物线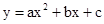 的解析式; 的解析式;
试判断直线CM与以AB为直径的圆的位置关系,并加以证明;
在抛物线上是否存在点N,使得 ?如果存在,那么这样的点有几个?如果不存在,请说明理由。 ?如果存在,那么这样的点有几个?如果不存在,请说明理由。 |
题型:解答题 难度:中档
答案
解:(1)Rt△ACB中,OC⊥AB,AO=1,BO=4,
∴△ACO∽△ABO 。∴ ,∴OC2=OA?OB=4。 ,∴OC2=OA?OB=4。
∴OC=2。∴点C(0,2)。
∵抛物线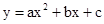 经过A、B两点, 经过A、B两点,
∴设抛物线的解析式为: ,将C点代入上式,得: ,将C点代入上式,得:
 ,解得 ,解得 。 。
∴抛物线的解析式: ,即 ,即 。 。
(2)直线CM与以AB为直径的圆相切。理由如下:
如图,设抛物线的对称轴与x轴的交点为D,连接CD。

由于A、B关于抛物线的对称轴对称,则点D为Rt△ABC斜边AB的中点,CD= AB。 AB。
由(1)知: , ,
则点M( ),ME= ),ME= 。 。
而CE=OD= ,OC=2,∴ME:CE=OD:OC。 ,OC=2,∴ME:CE=OD:OC。
又∵∠MEC=∠COD=90°,∴△COD∽△CEM。∴∠CME=∠CDO。
∴∠CME+∠CDM=∠CDO+∠CDM=90°。∠DCM=90°。
∵CD是⊙D的半径,∴直线CM与以AB为直径的圆相切。
(3)由B(4,0)、C(0,2)得:BC= , ,
则: 。 。
过点B作BF⊥BC,且使BF=h= ,过F作直线l∥BC交x轴于G。 ,过F作直线l∥BC交x轴于G。

Rt△BFG中,sin∠BGF=sin∠CBO= , ,
BG=BF÷sin∠BGF= 。 。
∴G(0,0)或(8,0)。
易知直线BC:y= x+2,则可设直线l:y= x+2,则可设直线l:y= x+b, x+b,
将G点坐标代入,得:b=0或b=4,则:
直线l:y= x或y= x或y= x+4; x+4;
联立抛物线的解析式,得:
 ,或 ,或 。 。
解得 或 或 或 或 。 。
∴抛物线上存在点N,使得 ,这样的点有3个: ,这样的点有3个:
 。 。 |
二次函数综合题,待定系数法,曲线上点的坐标与方程的关系,相似三角形的判定和性质,二次函数的性质,直线与的位置关系,平行线的性质。
【分析】(1)Rt△ACB中,OC⊥AB,利用相似三角形能求出OC的长,即可确定C点坐标,再利用待定系数法能求出该抛物线的解析式。
(2)证明CM垂直于过点C的半径即可。
(3)先求出线段BC的长,根据△BCN的面积,可求出BC边上的高,那么做直线l,且直线l与直线BC的长度正好等于BC边上的高,那么直线l与抛物线的交点即为符合条件的N点。 |
据专家权威分析,试题“如图14,已知点A(-1,0),B(4,0),点C在y轴的正半轴上,且∠ACB=..”主要考查你对 二次函数的定义,二次函数的图像,二次函数的最大值和最小值,求二次函数的解析式及二次函数的应用 等考点的理解。关于这些考点的“档案”如下:
二次函数的定义二次函数的图像二次函数的最大值和最小值求二次函数的解析式及二次函数的应用
考点名称:二次函数的定义 考点名称:二次函数的图像 考点名称:二次函数的最大值和最小值 考点名称:求二次函数的解析式及二次函数的应用
|

