|
题文
如图,在平面直角坐标系xOy中,AB⊥x轴于点B,AB=3,tan∠AOB=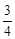 ,将△OAB绕着原点O逆时针旋转90°,得到△OA1B1;再将△OA1B1绕着线段OB1的中点旋转180°,得到△OA2B1,抛物线y=ax2+bx+c(a≠0)经过点B、B1、A2. ,将△OAB绕着原点O逆时针旋转90°,得到△OA1B1;再将△OA1B1绕着线段OB1的中点旋转180°,得到△OA2B1,抛物线y=ax2+bx+c(a≠0)经过点B、B1、A2.
(1)求抛物线的解析式.
(2)在第三象限内,抛物线上的点P在什么位置时,△PBB1的面积最大?求出这时点P的坐标.
(3)在第三象限内,抛物线上是否存在点Q,使点Q到线段BB1的距离为 ?若存在,求出点Q的坐标;若不存在,请说明理由. ?若存在,求出点Q的坐标;若不存在,请说明理由. |
题型:解答题 难度:偏难
答案
(1) (2)P(﹣2, (2)P(﹣2, )(3)存在,(﹣1,﹣4)或(﹣3,﹣2) )(3)存在,(﹣1,﹣4)或(﹣3,﹣2) |
解:(1)∵AB⊥x轴,AB=3,tan∠AOB=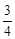 ,∴OB=4。 ,∴OB=4。
∴B(﹣4,0),B1(0,﹣4),A2(3,0)。
∵抛物线y=ax2+bx+c(a≠0)经过点B、B1、A2,
∴ ,解得 ,解得 。 。
∴抛物线的解析式为: 。 。
(2)点P是第三象限内抛物线 上的一点, 上的一点,
如图,过点P作PC⊥x轴于点C.

设点P的坐标为(m,n),
则m<0,n<0, 。 。
∴PC=|n|=﹣ ,OC=|m|=﹣m, ,OC=|m|=﹣m,
BC=OB﹣OC=|﹣4|﹣|m|=4+m。
∴

∴当m=﹣2时,△PBB1的面积最大,这时,n= ,即点P(﹣2, ,即点P(﹣2, )。 )。
(3)存在。
假设在第三象限的抛物线上存在点Q(x0,y0),使点Q到线段BB1的距离为 。 。
如图,过点Q作QD⊥BB1于点D,设Q(xQ,yQ),

由(2)可知,此时△QBB1的面积可以表示为:
 , ,
在Rt△OBB1中, 。 。
∵ , ,
∴ ,解得xQ=﹣1或xQ=﹣3。 ,解得xQ=﹣1或xQ=﹣3。
当xQ=﹣1时,yQ=﹣4;当xQ=﹣3时,yQ=﹣2。
因此,在第三象限内,抛物线上存在点Q,使点Q到线段BB1的距离为 ,这样的点Q的坐标是(﹣1,﹣4)或(﹣3,﹣2)。 ,这样的点Q的坐标是(﹣1,﹣4)或(﹣3,﹣2)。
(1)根据旋转的性质确定点B、B1、A2三点的坐标,利用待定系数法求得抛物线的解析式。
(2)求出△PBB1的面积表达式,这是一个关于P点横坐标的二次函数,利用二次函数求极值的方法求出△PBB1面积的最大值。
(3)引用(2)问中三角形面积表达式的结论,利用此表达式表示出△QBB1的面积,然后解一元二次方程求得Q点的坐标。 |
据专家权威分析,试题“如图,在平面直角坐标系xOy中,AB⊥x轴于点B,AB=3,tan∠AOB=,将..”主要考查你对 二次函数的定义,二次函数的图像,二次函数的最大值和最小值,求二次函数的解析式及二次函数的应用 等考点的理解。关于这些考点的“档案”如下:
二次函数的定义二次函数的图像二次函数的最大值和最小值求二次函数的解析式及二次函数的应用
考点名称:二次函数的定义 考点名称:二次函数的图像 考点名称:二次函数的最大值和最小值 考点名称:求二次函数的解析式及二次函数的应用
|

