|
题文
题型:解答题 难度:偏难
答案
解:(1)∵PD∥AB,
∴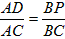 , ,
∵BC=4,AC= ,BP的长为x, ,BP的长为x,
∴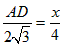 , ,
∴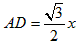 ; ;
(2)过点P作PE⊥AC于E,
∵ ,∠C=60°, ,∠C=60°,
∴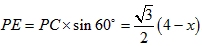 , ,
∴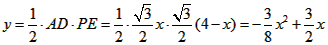 , ,
∴当x=2时,y的值最大,最大值是 ; ;
(3)点P存在这样的位置,
∵△ADP与△ABP等高不等底,
∴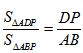 , ,
∵△ADP的面积是△ABP面积的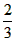 , ,
∴ , ,
∴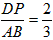 , ,
∵PD∥AB,
∴△CDP∽△CAB,
∴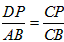 , ,
∴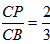 , ,
∴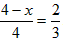 , ,
∴ , ,
∴ 。 。
 |
据专家权威分析,试题“如图,在△ABC中,∠C=60°,BC=4,AC=,点P在BC边上运动,PD∥AB,交..”主要考查你对 二次函数的最大值和最小值,相似三角形的性质,解直角三角形 等考点的理解。关于这些考点的“档案”如下:
二次函数的最大值和最小值相似三角形的性质解直角三角形
考点名称:二次函数的最大值和最小值 考点名称:相似三角形的性质 考点名称:解直角三角形
|

