|
题文
| 如图1,已知矩形ABCD的顶点A与点O重合,AD、AB分别在x轴、y轴上,且AD=2,AB=3;抛物线y=-x2+bx+c经过坐标原点O和x轴上另一点E(4,0)。 |
|
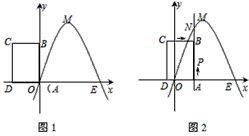
|
(1)当x取何值时,该抛物线有最大值,这个最大值是多少?
(2)将矩形ABCD以每秒1个单位长度的速度从图1所示的位置沿x轴的正方向匀速平行移动,同时一动点P也以相同的速度从点A出发向B匀速移动,设它们运动的时间为t秒(0≤t≤3),直线AB与该抛物线的交点为N(如图2所示),
①当 时,判断点P是否在直线ME上,并说明理由; 时,判断点P是否在直线ME上,并说明理由;
②以P、N、C、D为顶点的多边形面积是否可能为5,若有可能,求出此时N点的坐标;若无可能,请说明理由。 |
题型:解答题 难度:偏难
答案
解:(1)因抛物线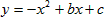 经过坐标原点O(0,0)和点E(4,0)故可得c=0,b=4, 经过坐标原点O(0,0)和点E(4,0)故可得c=0,b=4,
所以抛物线的解析式为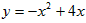 ,由 ,由 , ,
得当x=2时,该抛物线的最大值是4;
(2)①点P不在直线ME上,
已知M点的坐标为(2,4),E点的坐标为(4,0),
设直线ME的关系式为y=kx+b,
于是得 ,解得 ,解得 , ,
所以直线ME的关系式为y=-2x+8,
由已知条件易得,当 时,OA=AP= 时,OA=AP= ,P ,P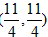 , ,
∵P点的坐标不满足直线ME的关系式y=-2x+8,
∴当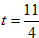 时,点P不在直线ME上; 时,点P不在直线ME上;
②以P、N、C、D为顶点的多边形面积可能为5,
∵点A在x轴的非负半轴上,且N在抛物线上,
∴OA=AP=t,
∴点P,N的坐标分别为(t,t)、(t,-t2+4t),
∴AN=-t2+4t(0≤t≤3),
∴AN-AP=(-t2+4t)-t=-t2+3t=t(3-t)≥0,
∴PN=-t2+3t,
(ⅰ)当PN=0,即t=0或t=3时,以点P,N,C,D为顶点的多边形是三角形,此三角形的高为AD,
∴S=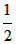 DC·AD= DC·AD=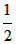 ×3×2=3; ×3×2=3;
(ⅱ)当PN≠0时,以点P,N,C,D为顶点的多边形是四边形,
∵PN∥CD,AD⊥CD,
∴S=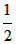 (CD+PN)·AD= (CD+PN)·AD=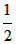 [3+(-t2+3t)]×2=-t2+3t+3, [3+(-t2+3t)]×2=-t2+3t+3,
当-t2+3t+3=5时,解得t=1、2,
而1、2都在0≤t≤3范围内,故以P、N、C、D为顶点的多边形面积为5,
综上所述,当t=1、2时,以点P,N,C,D为顶点的多边形面积为5,
当t=1时,此时N点的坐标(1,3),
当t=2时,此时N点的坐标(2,4)。 |
据专家权威分析,试题“如图1,已知矩形ABCD的顶点A与点O重合,AD、AB分别在x轴、y轴上,..”主要考查你对 二次函数的最大值和最小值,求一次函数的解析式及一次函数的应用,求二次函数的解析式及二次函数的应用 等考点的理解。关于这些考点的“档案”如下:
二次函数的最大值和最小值求一次函数的解析式及一次函数的应用求二次函数的解析式及二次函数的应用
考点名称:二次函数的最大值和最小值 考点名称:求一次函数的解析式及一次函数的应用 考点名称:求二次函数的解析式及二次函数的应用
|

