如图，在平面直角坐标系中，将一块腰长为的等腰直角三角板ABC放在第二象限，且斜靠在两坐标轴上，直角顶点C的坐标为（-1，0），点B在抛物线y=ax2+ax-2上。（1）点A的坐标为，点B-九年级数学打印页面

首页 > 考试 > 数学 > 初中数学 > 求二次函数的解析式及二次函数的应用 > 正文

如图，在平面直角坐标系中，将一块腰长为的等腰直角三角板ABC放在第二象限，且斜靠在两坐标轴上，直角顶点C的坐标为（-1，0），点B在抛物线y=ax2+ax-2上。（1）点A的坐标为，点B-九年级数学

[db:作者] 2019-12-17 00:00:00 零零社区

题文

如图，在平面直角坐标系中，将一块腰长为的等腰直角三角板ABC放在第二象限，且斜靠在两坐标轴上，直角顶点C的坐标为（-1，0），点B在抛物线y=ax²+ax-2 上。
（1）点A的坐标为          ，点B的坐标为          ；
（2）抛物线的关系式为          ；
（3）设（2）中抛物线的顶点为D，求△DBC的面积；
（4）将三角板ABC绕顶点A逆时针方向旋转90°，到达△AB'C' 的位置．请判断点B'、C' 是否在（2）中的抛物线上，并说明理由。

题型：解答题  难度：偏难

答案

解：（1）A（0，2）， B（-3，1）
（2）
（3）可求得抛物线的顶点D（）
设直线BD的关系式为，将点B、D的坐标代入，求得，
∴ BD的关系式为
设直线BD和x 轴交点为E，则点E（，0），CE=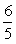
∴ △DBC的面积为
（4）过点B'作B'M⊥y轴于点M，过点B作BN⊥Y轴于点N，过点C'作C'P⊥y轴于点P
在Rt△AB'M与Rt△BAN中， ∵ AB=AB′， ∠AB'M=∠BAN=90°-∠B'AM
∴ Rt△AB'M≌Rt△BAN
∴ B'M=AN=1，AM=BN=3， ∴ B′（1，-1）
同理△AC'P≌△CAO，C'P=OA=2，AP=OC=1，可得点C'（2，1）
将点B'、C'的坐标代入，可知点B'、C'在抛物线上
（事实上点P与点N重合）

据专家权威分析，试题“如图，在平面直角坐标系中，将一块腰长为的等腰直角三角板ABC放在..”主要考查你对求二次函数的解析式及二次函数的应用，二次函数的图像，全等三角形的性质，勾股定理等考点的理解。关于这些考点的“档案”如下：

求二次函数的解析式及二次函数的应用二次函数的图像全等三角形的性质勾股定理

考点名称：求二次函数的解析式及二次函数的应用

求二次函数的解析式：
最常用的方法是待定系数法，根据题目的特点，选择恰当的形式，一般，有如下几种情况：
（1）已知抛物线上三点的坐标，一般选用一般式；
（2）已知抛物线顶点或对称轴或最大（小）值，一般选用顶点式；
（3）已知抛物线与x轴的两个交点的横坐标，一般选用两点式；
（4）已知抛物线上纵坐标相同的两点，常选用顶点式。

二次函数的应用：
（1）应用二次函数才解决实际问题的一般思路：
理解题意；
建立数学模型；
解决题目提出的问题。
（2）应用二次函数求实际问题中的最值：
即解二次函数最值应用题，设法把关于最值的实际问题转化为二次函数的最值问题，然后按求二次函数最值的方法求解。
求最值时，要注意求得答案要符合实际问题。
二次函数的三种表达形式：
①一般式：
y=ax2+bx+c(a≠0,a、b、c为常数)，顶点坐标为 [,]
把三个点代入函数解析式得出一个三元一次方程组，就能解出a、b、c的值。

②顶点式：
y=a(x-h)2+k(a≠0,a、h、k为常数),顶点坐标为对称轴为直线x=h，顶点的位置特征和图像的开口方向与函数y=ax²的图像相同，当x=h时，y最值=k。
有时题目会指出让你用配方法把一般式化成顶点式。
例：已知二次函数y的顶点(1,2)和另一任意点(3,10)，求y的解析式。
解：设y=a(x-1)2+2，把(3,10)代入上式，解得y=2(x-1)2+2。
注意：与点在平面直角坐标系中的平移不同，二次函数平移后的顶点式中，h>0时，h越大，图像的对称轴离y轴越远，且在x轴正方向上，不能因h前是负号就简单地认为是向左平移。
具体可分为下面几种情况：
当h>0时，y=a(x-h)2的图象可由抛物线y=ax2向右平行移动h个单位得到；
当h<0时，y=a(x-h)2的图象可由抛物线y=ax2向左平行移动|h|个单位得到；
当h>0,k>0时，将抛物线y=ax2向右平行移动h个单位，再向上移动k个单位，就可以得到y=a(x-h)2+k的图象；
当h>0,k<0时，将抛物线y=ax2向右平行移动h个单位，再向下移动|k|个单位可得到y=a(x-h)2+k的图象；
当h<0,k>0时，将抛物线y=ax2向左平行移动|h|个单位，再向上移动k个单位可得到y=a(x-h)2+k的图象；
当h<0,k<0时，将抛物线y=ax2向左平行移动|h|个单位，再向下移动|k|个单位可得到y=a(x-h)2+k的图象。

③交点式：
y=a(x-x₁)(x-x₂) (a≠0) [仅限于与x轴即y=0有交点时的抛物线，即b²-4ac≥0] .
已知抛物线与x轴即y=0有交点A（x₁，0）和 B（x₂，0）,我们可设y=a(x-x₁)(x-x₂),然后把第三点代入x、y中便可求出a。

由一般式变为交点式的步骤：
二次函数
∵x₁+x₂=-b/a， x₁?x₂=c/a(由韦达定理得),
∴y=ax2+bx+c
=a(x2+b/ax+c/a)
=a[x2-(x₁+x₂)x+x₁?x₂]
=a(x-x₁)(x-x₂).
重要概念：
a，b，c为常数，a≠0，且a决定函数的开口方向。a>0时，开口方向向上；
a<0时，开口方向向下。a的绝对值可以决定开口大小。
a的绝对值越大开口就越小，a的绝对值越小开口就越大。
能灵活运用这三种方式求二次函数的解析式；
能熟练地运用二次函数在几何领域中的应用；
能熟练地运用二次函数解决实际问题。
二次函数的其他表达形式：
①牛顿插值公式:
f(x)=f[x₀]+f[x₀,x₁](x-x₀)+f[x₀,x₁,x₂](x-x₀)(x-x₁)+...f[x₀,...x_n](x-x₀)...(x-_xn-1)+Rn(x)由此可引导出交点式的系数a=y/(x·x)(y为截距)　
二次函数表达式的右边通常为二次三项式。

双根式
y=a(x-x₁)*(x-x2)
若ax2+bx+c=0有两个实根x₁,x₂，则y=a(x-x₁)(x-x₂)此抛物线的对称轴为直线x=(x₁+x₂)/2。

③三点式
已知二次函数上三个点，（x₁,f(x₁)）（x₂,f(x₂)）（x₃,f(x₃)）
则f(x)=f(x₃)(x-x₁)(x-x₂)/(x₃-x₁)(x₃-x₂)+f(x₂)(x-x₁)*(x-x₃)/(x₂-x₁)(x₂-x₃)+f(x₁)(x-x₂)(x-x₃)/(x₁-x₂)(x₁-x₃)
与X轴交点的情况
当△=b2-4ac>0时，函数图像与x轴有两个交点。(x₁,0), (x₂,0);
当△=b2-4ac=0时，函数图像与x轴只有一个交点。(-b/2a，0)。
Δ=b2-4ac<0时，抛物线与x轴没有交点。
X的取值是虚数（x=-b±√b2－4ac的值的相反数，乘上虚数i，整个式子除以2a）
二次函数解释式的求法：
就一般式y=ax2＋bx＋c（其中a，b，c为常数，且a≠0）而言，其中含有三个待定的系数a ，b ，c．求二次函数的一般式时，必须要有三个独立的定量条件，来建立关于a ，b ，c 的方程，联立求解，再把求出的a ，b ，c 的值反代回原函数解析式，即可得到所求的二次函数解析式。

1.巧取交点式法：
知识归纳：二次函数交点式：y＝a(x－x₁)(x－x₂) （a≠0）x₁，x₂分别是抛物线与x轴两个交点的横坐标。
已知抛物线与x轴两个交点的横坐标求二次函数解析式时，用交点式比较简便。
①典型例题一：告诉抛物线与x轴的两个交点的横坐标，和第三个点，可求出函数的交点式。
例：已知抛物线与x轴交点的横坐标为-2和1 ，且通过点（2，8），求二次函数的解析式。
点拨：
解设函数的解析式为y＝a(x+2)(x-1)，
∵过点（2，8），
∴8＝a(2+2)(2-1)。
解得a=2，
∴抛物线的解析式为：
y＝2(x+2)(x-1)，
即y＝2x2+2x-4。

②典型例题二：告诉抛物线与x轴的两个交点之间的距离和对称轴，可利用抛物线的对称性求解。
例：已知二次函数的顶点坐标为（3，-2），并且图象与x轴两交点间的距离为4，求二次函数的解析式。
点拨：
在已知抛物线与x轴两交点的距离和顶点坐标的情况下，问题比较容易解决．由顶点坐标为（3，-2）的条件，易知其对称轴为x＝3，再利用抛物线的对称性，可知图象与x轴两交点的坐标分别为（1，0）和（5，0）。此时，可使用二次函数的交点式，得出函数解析式。

2.巧用顶点式：
顶点式y=a(x－h)²+k（a≠0），其中（h，k）是抛物线的顶点。当已知抛物线顶点坐标或对称轴，或能够先求出抛物线顶点时，设顶点式解题十分简洁，因为其中只有一个未知数a。在此类问题中，常和对称轴，最大值或最小值结合起来命题。在应用题中，涉及到桥拱、隧道、弹道曲线、投篮等问题时，一般用顶点式方便．
①典型例题一：告诉顶点坐标和另一个点的坐标，直接可以解出函数顶点式。
例：已知抛物线的顶点坐标为（-1，-2），且通过点（1，10），求此二次函数的解析式。
点拨：
解∵顶点坐标为（-1，-2），
故设二次函数解析式为y=a(x+1)²-2 （a≠0）。
把点（1，10）代入上式，得10=a·(1+1)²-2。
∴a=3。
∴二次函数的解析式为y=3(x+1)²-2，即y=3x²+6x+1。

②典型例题二：
如果a>0，那么当时，y有最小值且y_最小=；
如果a<0，那么，当时，y有最大值，且y_最大=。
告诉最大值或最小值，实际上也是告诉了顶点坐标，同样也可以求出顶点式。
例：已知二次函数当x＝4时有最小值－3，且它的图象与x轴两交点间的距离为6，求这个二次函数的解析式。
点拨：
析解∵二次函数当x＝4时有最小值－3，∴顶点坐标为（4，-3），对称轴为直线x＝4，抛物线开口向上。
由于图象与x轴两交点间的距离为6，根据图象的对称性就可以得到图象与x轴两交点的坐标是（1，0）和（7，0）。
∴抛物线的顶点为（4，-3）且过点（1，0）。
故可设函数解析式为y＝a(x－4)²－3。
将（1，0）代入得0＝a(1－4)²－3, 解得a＝13．
∴y＝13(x－4)²-3，即y＝13x²－83x＋73。
③典型例题三：告诉对称轴，相当于告诉了顶点的横坐标，综合其他条件，也可解出。
例如：
（1）已知二次函数的图象经过点A（3，-2）和B（1，0），且对称轴是直线x＝3．求这个二次函数的解析式.
（2）已知关于x的二次函数图象的对称轴是直线x=1，图象交y轴于点（0，2），且过点（-1，0），求这个二次函数的解析式.
（3）已知抛物线的对称轴为直线x=2，且通过点（1，4）和点（5，0），求此抛物线的解析式.
（4）二次函数的图象的对称轴x=-4，且过原点，它的顶点到x轴的距离为4，求此函数的解析式．

④典型例题四：利用函数的顶点式，解图像的平移等问题非常方便。
例：把抛物线y=ax2+bx+c的图像向右平移3 个单位, 再向下平移2 个单位, 所得图像的解析式是y=x2-3x+5, 则函数的解析式为_______。
点拨：
解先将y=x2-3x+5化为y=(x-32)2+5-94, 即y=(x-32)2+114。
∵它是由抛物线的图像向右平移3 个单位, 再向下平移2 个单位得到的，
∴原抛物线的解析式是y=(x-32+3)2+114+2=(x+32)2+194=x2+3x+7。

考点名称：二次函数的图像

二次函数的图像
是一条关于对称的曲线，这条曲线叫抛物线。
抛物线的主要特征：
①有开口方向，a表示开口方向：a>0时，抛物线开口向上；a<0时，抛物线开口向下；
②有对称轴；
③有顶点；
④c 表示抛物线与y轴的交点坐标：（0，c）。
二次函数图像性质：
轴对称：
二次函数图像是轴对称图形。对称轴为直线x=-b/2a
对称轴与二次函数图像唯一的交点为二次函数图像的顶点P。
特别地，当b=0时，二次函数图像的对称轴是y轴（即直线x=0）。
a,b同号，对称轴在y轴左侧
b=0,对称轴是y轴
a,b异号，对称轴在y轴右侧

顶点：
二次函数图像有一个顶点P，坐标为P ( h,k )
当h=0时，P在y轴上；当k=0时，P在x轴上。即可表示为顶点式y=a(x-h)^2+k。
h=-b/2a， k=(4ac-b^2)/4a。

开口：
二次项系数a决定二次函数图像的开口方向和大小。
当a>0时，二次函数图像向上开口；当a<0时，抛物线向下开口。
|a|越大，则二次函数图像的开口越小。
决定对称轴位置的因素：
一次项系数b和二次项系数a共同决定对称轴的位置。
当a>0,与b同号时（即ab>0），对称轴在y轴左；因为对称轴在左边则对称轴小于0，也就是- b/2a<0,所以 b/2a要大于0，所以a、b要同号
当a>0,与b异号时（即ab<0），对称轴在y轴右。因为对称轴在右边则对称轴要大于0，也就是- b/2a>0, 所以b/2a要小于0，所以a、b要异号
可简单记忆为左同右异，即当a与b同号时（即ab>0），对称轴在y轴左；当a与b异号时（即ab<0 ），对称轴在y轴右。
事实上，b有其自身的几何意义：二次函数图像与y轴的交点处的该二次函数图像切线的函数解析式（一次函数）的斜率k的值。可通过对二次函数求导得到。

决定与y轴交点的因素:
常数项c决定二次函数图像与y轴交点。
二次函数图像与y轴交于（0,C）
注意：顶点坐标为（h,k)，与y轴交于（0,C)。

与x轴交点个数：
a<0;k>0或a>0;k<0时，二次函数图像与x轴有2个交点。
k=0时，二次函数图像与x轴只有1个交点。
a<0;k<0或a>0,k>0时，二次函数图像与X轴无交点。
当a>0时，函数在x=h处取得最小值ymin=k，在x<h范围内是减函数，在x>h范围内是增函数（即y随x的变大而变小），二次函数图像的开口向上，函数的值域是y>k
当a<0时，函数在x=h处取得最大值ymax=k，在x<h范围内是增函数，在x>h范围内是减函数（即y随x的变大而变大），二次函数图像的开口向下，函数的值域是y<k
当h=0时，抛物线的对称轴是y轴，这时，函数是偶函数。

考点名称：全等三角形的性质

全等三角形：
两个全等的三角形，而该两个三角形的三条边及三个角都对应地相等。全等三角形是几何中全等的一种。根据全等转换，两个全等三角形可以是平移、旋转、轴对称，或重叠等。当两个三角形的对应边及角都完全相对时，该两个三角形就是全等三角形。正常来说，验证两个全等三角形时都以三个相等部分来验证，最后便能得出结果。
全等三角形的对应边相等，对应角相等。
①全等三角形对应角所对的边是对应边，两个对应角所夹的边是对应边;
②全等三角形对应边所对的角是对应角，两条对应边所夹的角是对应角;
③有公共边的，公共边一定是对应边;
④有公共角的，角一定是对应角;
⑤有对顶角的，对顶角一定是对应角。
全等三角形的性质：
1.全等三角形的对应角相等。
2.全等三角形的对应边相等。
3.全等三角形的对应边上的高对应相等。
4.全等三角形的对应角的角平分线相等。
5.全等三角形的对应边上的中线相等。
6.全等三角形面积相等。
7.全等三角形周长相等。
8.全等三角形的对应角的三角函数值相等。

考点名称：勾股定理

勾股定理:
直角三角形两直角边(即“勾”，“股”)边长平方和等于斜边(即“弦”)边长的平方。也就是说，如果直角三角形的两直角边长分别为a，b，斜边长为c，那么。
勾股定理只适用于直角三角形，应用于解决直角三角形中的线段求值问题。
定理作用
⑴勾股定理是联系数学中最基本也是最原始的两个对象——数与形的第一定理。
⑵勾股定理导致不可通约量的发现，从而深刻揭示了数与量的区别，即所谓“无理数"与有理数的差别，这就是所谓第一次数学危机。
⑶勾股定理开始把数学由计算与测量的技术转变为证明与推理的科学。
⑷勾股定理中的公式是第一个不定方程，也是最早得出完整解答的不定方程，它一方面引导到各式各样的不定方程，包括著名的费尔马大定理，另一方面也为不定方程的解题程序树立了一个范式。
勾股定理的应用：
数学
从勾股定理出发开平方、开立方、求圆周率等，运用勾股定理数学家还发现了无理数。
勾股定理在几何学中的实际应用非常广泛，较早的应用案例有《九章算术》中的一题：“今有池，芳一丈，薛生其中央，出水一尺，引薛赴岸，适与岸齐，问水深几何？答曰："一十二尺"。

生活
勾股定理在生活中的应用也较广泛，举例说明如下：
1、挑选投影设备时需要选择最佳的投影屏幕尺寸。以教室为例，最佳的屏幕尺寸主要取决于使用空间的面积，从而计划好学生座位的多少和位置的安排。选购的关键则是选择适合学生的屏幕而不是选择适合投影机的屏幕，也就是说要把学生的视觉感受放在第一位。一般来说在选购时可参照三点：
第一，屏幕高度大约等于从屏幕到学生最后一排座位的距离的1/6；
第二，屏幕到第一排座位的距离应大于2倍屏幕的高度；
第三，屏幕底部应离观众席所在地面最少122厘米。
屏幕的尺寸是以其对角线的大小来定义的。一般视频图像的宽高比为4:3，教育幕为正方形。如一个72英寸的屏幕，根据勾股定理，很快就能得出屏幕的宽为1.5m，高为1.1m。
2、2005年珠峰高度复测行动。
测量珠峰的一种方法是传统的经典测量方法，就是把高程引到珠峰脚下，当精确高程传递至珠峰脚下的6个峰顶交会测量点时，通过在峰顶竖立的测量觇标，运用“勾股定理”的基本原理测定珠峰高程，配合水准测量、三角测量、导线测量等方式，获得的数据进行重力、大气等多方面改正计算，最终得到珠峰高程的有效数据。
通俗来说，就是分三步走：
第一步，先在珠峰脚下选定较容易的、能够架设水准仪器的测量点，先把这些点的精确高程确定下来；
第二步，在珠峰峰顶架起觇标，运用三角几何学中“勾股定理”的基本原理，推算出珠峰峰顶相对于这几个点的高程差；
第三步，获得的高程数据要进行重力、大气等多方面的改正计算，最终确定珠峰高程测量的有效数据。

http://www.00-edu.com/ks/shuxue/2/120/2019-12-18/1874371.html十二生肖
十二星座