零零教育信息网 首页 > 考试 > 数学 > 初中数学 > 求二次函数的解析式及二次函数的应用 > 正文 返回　打印

如图，已知矩形ABCD的边长AB=2，BC=3，点P是AD边上的一动点（P异于A、D），Q是BC边上的任意一点.连AQ.DQ，过P作PE∥DQ交AQ于E，作PF∥AQ交DQ于F。（1）求证：△APE∽△ADQ；（2）设AP的-九年级数学
[db:作者]  2019-12-17 00:00:00  零零社区

题文

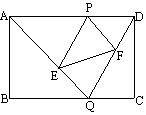
如图，已知矩形ABCD的边长AB=2，BC=3，点P是AD边上的一动点（P异于A、D），Q是BC边上的任意一点. 连AQ. DQ，过P作PE∥DQ交AQ于E，作PF∥AQ交DQ于F。
（1）求证：△APE∽△ADQ；
（2）设AP的长为x，试求△PEF的面积S△PEF关于x的函数关系式，并求当P在何处时，S△PEF取得最大值？最大值为多少？
（3）当Q在何处时，△ADQ的周长最小？（须给出确定Q在何处的过程或方法，不必给出证明）
题型：解答题  难度：中档

答案

解：（1）证明∠APE=∠ADQ，∠AEP=∠AQD（过程“略”）
（2）注意到△APE∽△ADQ与△PDE∽△ADQ，及S△PEF=
得S△PEF==
∴当，即P是AD的中点时，S△PEF取得最大值。
（3）作A关于直线BC的对称点A'，连DA'交BC于Q，则这个点Q就是使△ADQ周长最小的点，此时Q是BC的中点

据专家权威分析，试题“如图，已知矩形ABCD的边长AB=2，BC=3，点P是AD边上的一动点（P异于..”主要考查你对  求二次函数的解析式及二次函数的应用，相似三角形的判定  等考点的理解。关于这些考点的“档案”如下：

求二次函数的解析式及二次函数的应用相似三角形的判定

考点名称：求二次函数的解析式及二次函数的应用

  • 求二次函数的解析式：
    最常用的方法是待定系数法，根据题目的特点，选择恰当的形式，一般，有如下几种情况：
    （1）已知抛物线上三点的坐标，一般选用一般式；
    （2）已知抛物线顶点或对称轴或最大（小）值，一般选用顶点式；
    （3）已知抛物线与x轴的两个交点的横坐标，一般选用两点式；
    （4）已知抛物线上纵坐标相同的两点，常选用顶点式。

    二次函数的应用：
    （1）应用二次函数才解决实际问题的一般思路：
    理解题意；
    建立数学模型；
    解决题目提出的问题。
    （2）应用二次函数求实际问题中的最值：
    即解二次函数最值应用题，设法把关于最值的实际问题转化为二次函数的最值问题，然后按求二次函数最值的方法求解。
    求最值时，要注意求得答案要符合实际问题。

  • 二次函数的三种表达形式：
    ①一般式：
    y=ax2+bx+c(a≠0,a、b、c为常数)，顶点坐标为 [,]
    把三个点代入函数解析式得出一个三元一次方程组，就能解出a、b、c的值。

    ②顶点式：
    y=a(x-h)2+k(a≠0,a、h、k为常数),顶点坐标为对称轴为直线x=h，顶点的位置特征和图像的开口方向与函数y=ax2的图像相同，当x=h时，y最值=k。
    有时题目会指出让你用配方法把一般式化成顶点式。
    例：已知二次函数y的顶点(1,2)和另一任意点(3,10)，求y的解析式。
    解：设y=a(x-1)2+2，把(3,10)代入上式，解得y=2(x-1)2+2。
    注意：与点在平面直角坐标系中的平移不同，二次函数平移后的顶点式中，h>0时，h越大，图像的对称轴离y轴越远，且在x轴正方向上，不能因h前是负号就简单地认为是向左平移。
    具体可分为下面几种情况：
    当h>0时，y=a(x-h)2的图象可由抛物线y=ax2向右平行移动h个单位得到；
    当h<0时，y=a(x-h)2的图象可由抛物线y=ax2向左平行移动|h|个单位得到；
    当h>0,k>0时，将抛物线y=ax2向右平行移动h个单位，再向上移动k个单位，就可以得到y=a(x-h)2+k的图象；
    当h>0,k<0时，将抛物线y=ax2向右平行移动h个单位，再向下移动|k|个单位可得到y=a(x-h)2+k的图象；
    当h<0,k>0时，将抛物线y=ax2向左平行移动|h|个单位，再向上移动k个单位可得到y=a(x-h)2+k的图象；
    当h<0,k<0时，将抛物线y=ax2向左平行移动|h|个单位，再向下移动|k|个单位可得到y=a(x-h)2+k的图象。

    ③交点式：
    y=a(x-x1)(x-x2) (a≠0) [仅限于与x轴即y=0有交点时的抛物线，即b2-4ac≥0] .
    已知抛物线与x轴即y=0有交点A（x1，0）和 B（x2，0）,我们可设y=a(x-x1)(x-x2),然后把第三点代入x、y中便可求出a。

    由一般式变为交点式的步骤：
    二次函数
    ∵x1+x2=-b/a， x1?x2=c/a(由韦达定理得),
    ∴y=ax2+bx+c
    =a(x2+b/ax+c/a)
    =a[x2-(x1+x2)x+x1?x2]
    =a(x-x1)(x-x2).
    重要概念：
    a，b，c为常数，a≠0，且a决定函数的开口方向。a>0时，开口方向向上；
    a<0时，开口方向向下。a的绝对值可以决定开口大小。
    a的绝对值越大开口就越小，a的绝对值越小开口就越大。
    能灵活运用这三种方式求二次函数的解析式；
    能熟练地运用二次函数在几何领域中的应用；
    能熟练地运用二次函数解决实际问题。

  • 二次函数的其他表达形式：
    ①牛顿插值公式:
    f(x)=f[x0]+f[x0,x1](x-x0)+f[x0,x1,x2](x-x0)(x-x1)+...f[x0,...xn](x-x0)...(x-xn-1)+Rn(x)由此可引导出交点式的系数a=y/(x·x)(y为截距)　
    二次函数表达式的右边通常为二次三项式。

    双根式
    y=a(x-x1)*(x-x2)
    若ax2+bx+c=0有两个实根x1,x2，则y=a(x-x1)(x-x2)此抛物线的对称轴为直线x=(x1+x2)/2。

    ③三点式
    已知二次函数上三个点，（x1,f(x1)）（x2,f(x2)）（x3,f(x3)）
    则f(x)=f(x3)(x-x1)(x-x2)/(x3-x1)(x3-x2)+f(x2)(x-x1)*(x-x3)/(x2-x1)(x2-x3)+f(x1)(x-x2)(x-x3)/(x1-x2)(x1-x3)
    与X轴交点的情况
    当△=b2-4ac>0时，函数图像与x轴有两个交点。(x1,0), (x2,0);
    当△=b2-4ac=0时，函数图像与x轴只有一个交点。(-b/2a，0)。
    Δ=b2-4ac<0时，抛物线与x轴没有交点。
    X的取值是虚数（x=-b±√b2－4ac的值的相反数，乘上虚数i，整个式子除以2a）

  • 二次函数解释式的求法：
    就一般式y=ax2＋bx＋c（其中a，b，c为常数，且a≠0）而言，其中含有三个待定的系数a ，b ，c．求二次函数的一般式时，必须要有三个独立的定量条件，来建立关于a ，b ，c 的方程，联立求解，再把求出的a ，b ，c 的值反代回原函数解析式，即可得到所求的二次函数解析式。

    1.巧取交点式法：
    知识归纳：二次函数交点式：y＝a(x－x1)(x－x2) （a≠0）x1，x2分别是抛物线与x轴两个交点的横坐标。
    已知抛物线与x轴两个交点的横坐标求二次函数解析式时，用交点式比较简便。
    ①典型例题一：告诉抛物线与x轴的两个交点的横坐标，和第三个点，可求出函数的交点式。
    例：已知抛物线与x轴交点的横坐标为-2和1 ，且通过点（2，8），求二次函数的解析式。
    点拨：
    解设函数的解析式为y＝a(x+2)(x-1)，
    ∵过点（2，8），
    ∴8＝a(2+2)(2-1)。
    解得a=2，
    ∴抛物线的解析式为：
    y＝2(x+2)(x-1)，
    即y＝2x2+2x-4。

    ②典型例题二：告诉抛物线与x轴的两个交点之间的距离和对称轴，可利用抛物线的对称性求解。
    例：已知二次函数的顶点坐标为（3，-2），并且图象与x轴两交点间的距离为4，求二次函数的解析式。
    点拨：
    在已知抛物线与x轴两交点的距离和顶点坐标的情况下，问题比较容易解决．由顶点坐标为（3，-2）的条件，易知其对称轴为x＝3，再利用抛物线的对称性，可知图象与x轴两交点的坐标分别为（1，0）和（5，0）。此时，可使用二次函数的交点式，得出函数解析式。

    2.巧用顶点式：
    顶点式y=a(x－h)2+k（a≠0），其中（h，k）是抛物线的顶点。当已知抛物线顶点坐标或对称轴，或能够先求出抛物线顶点时，设顶点式解题十分简洁，因为其中只有一个未知数a。在此类问题中，常和对称轴，最大值或最小值结合起来命题。在应用题中，涉及到桥拱、隧道、弹道曲线、投篮等问题时，一般用顶点式方便．
    ①典型例题一：告诉顶点坐标和另一个点的坐标，直接可以解出函数顶点式。
    例：已知抛物线的顶点坐标为（-1，-2），且通过点（1，10），求此二次函数的解析式。
    点拨：
    解∵顶点坐标为（-1，-2），
    故设二次函数解析式为y=a(x+1)2-2 （a≠0）。
    把点（1，10）代入上式，得10=a·(1+1)2-2。
    ∴a=3。
    ∴二次函数的解析式为y=3(x+1)2-2，即y=3x2+6x+1。

    ②典型例题二：
    如果a>0，那么当 时，y有最小值且y最小=；
    如果a<0，那么，当时，y有最大值，且y最大=。
    告诉最大值或最小值，实际上也是告诉了顶点坐标，同样也可以求出顶点式。
    例：已知二次函数当x＝4时有最小值－3，且它的图象与x轴两交点间的距离为6，求这个二次函数的解析式。
    点拨：
    析解∵二次函数当x＝4时有最小值－3，∴顶点坐标为（4，-3），对称轴为直线x＝4，抛物线开口向上。
    由于图象与x轴两交点间的距离为6，根据图象的对称性就可以得到图象与x轴两交点的坐标是（1，0）和（7，0）。
    ∴抛物线的顶点为（4，-3）且过点（1，0）。
    故可设函数解析式为y＝a(x－4)2－3。
    将（1，0）代入得0＝a(1－4)2－3, 解得a＝13．
    ∴y＝13(x－4)2-3，即y＝13x2－83x＋73。
    ③典型例题三：告诉对称轴，相当于告诉了顶点的横坐标，综合其他条件，也可解出。
    例如：
    （1）已知二次函数的图象经过点A（3，-2）和B（1，0），且对称轴是直线x＝3．求这个二次函数的解析式.
    （2）已知关于x的二次函数图象的对称轴是直线x=1，图象交y轴于点（0，2），且过点（-1，0），求这个二次函数的解析式.
    （3）已知抛物线的对称轴为直线x=2，且通过点（1，4）和点（5，0），求此抛物线的解析式.
    （4）二次函数的图象的对称轴x=-4，且过原点，它的顶点到x轴的距离为4，求此函数的解析式．

    ④典型例题四：利用函数的顶点式，解图像的平移等问题非常方便。
    例：把抛物线y=ax2+bx+c的图像向右平移3 个单位, 再向下平移2 个单位, 所得图像的解析式是y=x2-3x+5, 则函数的解析式为_______。
    点拨：
    解先将y=x2-3x+5化为y=(x-32)2+5-94, 即y=(x-32)2+114。
    ∵它是由抛物线的图像向右平移3 个单位, 再向下平移2 个单位得到的，
    ∴原抛物线的解析式是y=(x-32+3)2+114+2=(x+32)2+194=x2+3x+7。

考点名称：相似三角形的判定

  • 相似三角形：
    对应角相等，对应边成比例的两个三角形叫做相似三角形。
    互为相似形的三角形叫做相似三角形。

    例如图中，若B'C'//BC，那么角B=角B'，角BAC=角B'A'C'，是对顶角，那么我们就说△ABC∽△AB'C'

  • 相似三角形的判定：
    1.基本判定定理
    (1)平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似。
    (2)如果一个三角形的两条边和另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似。(简叙为：两边对应成比例且夹角相等，两个三角形相似。)
    (3)如果一个三角形的三条边与另一个三角形的三条边对应成比例，那么这两个三角形相似。(简叙为：三边对应成比例，两个三角形相似。)
    (4)如果两个三角形的两个角分别对应相等（或三个角分别对应相等），那么这两个三角形相似。
    2.直角三角形判定定理
    (1)直角三角形被斜边上的高分成两个直角三角形和原三角形相似。
    (2)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似。
    3.一定相似：
    （1）.两个全等的三角形
    （全等三角形是特殊的相似三角形，相似比为1：1）
    （2）.两个等腰三角形
    （两个等腰三角形，如果其中的任意一个顶角或底角相等，那么这两个等腰三角形相似。）
    （3）.两个等边三角形
    (两个等边三角形，三个内角都是60度，且边边相等，所以相似)　
    （4）.直角三角形中由斜边的高形成的三个三角形。

  • 相似三角形判定方法：
    证两个相似三角形应该把表示对应顶点的字母写在对应的位置上。如果是文字语言的“△ABC与△DEF相似”，那么就说明这两个三角形的对应顶点可能没有写在对应的位置上，而如果是符号语言的“△ABC∽△DEF”，那么就说明这两个三角形的对应顶点写在了对应的位置上。
    一、（预备定理）
    平行于三角形一边的直线截其它两边所在的直线，截得的三角形与原三角形相似。（这是相似三角形判定的定理，是以下判定方法证明的基础。这个引理的证明方法需要平行线与线段成比例的证明）
    二、如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。
    三、如果两个三角形的两组对应边成比例，并且相应的夹角相等,那么这两个三角形相似。 
    四、如果两个三角形的三组对应边成比例，那么这两个三角形相似
    五（定义）
    对应角相等，对应边成比例的两个三角形叫做相似三角形
    六、两三角形三边对应垂直，则两三角形相似。
    七、两个直角三角形中，斜边与直角边对应成比例，那么两三角形相似。
    八、由角度比转化为线段比：h1/h2=Sabc

    易失误
    比值是一个具体的数字如：AB/EF=2
    而比不是一个具体的数字如：AB/EF=2：1
http://www.00-edu.com/ks/shuxue/2/120/2019-12-18/1874388.html十二生肖
十二星座