| 如图,△ABC中,AC=BC,∠A=30°,AB=,现将一块三角板中30°角的顶点D放在AB边上移动,使这个30°角的两边分别与△ABC的边AC,BC相交于点E,F,连结DE,DF,EF,且使DE始终与AB垂直-九年级数学 |
|
[db:作者] 2019-12-17 00:00:00 零零社区 |
|
|
题文
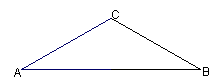
如图,△ABC中,AC=BC,∠A=30°,AB=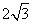 ,现将一块三角板中30°角的顶点D放在AB边上移动,使这个 30°角的两边分别与△ABC的边AC,BC相交于点E, F,连结DE,DF,EF,且使DE始终与AB垂直,设AD=x,△DEF的面积为y。 ,现将一块三角板中30°角的顶点D放在AB边上移动,使这个 30°角的两边分别与△ABC的边AC,BC相交于点E, F,连结DE,DF,EF,且使DE始终与AB垂直,设AD=x,△DEF的面积为y。
(1)画出符合条件的图形,写出与△ADE一定相似的三角形(不包括此三角板),并说明理由;
(2)问EF与AB可能平行吗?若能,请求出此时AD的长;若不能,请说明理由;
(3)求出y与x之间的函数关系式,并写出自变量x的取值范围,当x为何值时,y有最大值?最大值是为多少? |
|
|
题型:解答题 难度:偏难
答案
解:(1)图形举例: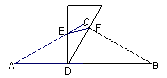
△ADE∽△BFD,
∵ DE⊥AB,∠EDF=30°,
∴∠FDB=60°,
∵ ∠A=∠B,∠AED=∠FDB,
∴ △ADE∽△BFD,(答案不唯一);
(2)EF可以平行于AB,
此时,在直角△ADE中,DE= , ,
在直角△DEF中,EF=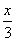 , ,
在直角△DBF中, ∵ BD=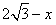 , ∴ DF= , ∴ DF=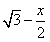 , ,
而DF=2EF, ∴ = =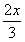 , ,
∴
(3)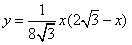 ,即 ,即 , ,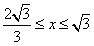
当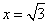 时,y最大= 时,y最大=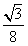 |
 |
据专家权威分析,试题“如图,△ABC中,AC=BC,∠A=30°,AB=,现将一块三角板中30°角的顶点..”主要考查你对 求二次函数的解析式及二次函数的应用,平行线的判定,相似三角形的判定 等考点的理解。关于这些考点的“档案”如下:
求二次函数的解析式及二次函数的应用平行线的判定相似三角形的判定
考点名称:求二次函数的解析式及二次函数的应用 考点名称:平行线的判定 考点名称:相似三角形的判定
|
|
http://www.00-edu.com/ks/shuxue/2/120/2019-12-18/1874465.html十二生肖十二星座
|

