凯里市某大型酒店有包房100间，在每天晚餐营业时间，每间包房收包房费100元时，包房便可全部租出。若每间包房收费提高20元，则减少10间包房租出；若每间包房收费再提高20元，-九年级数学打印页面

首页 > 考试 > 数学 > 初中数学 > 求二次函数的解析式及二次函数的应用 > 正文

凯里市某大型酒店有包房100间，在每天晚餐营业时间，每间包房收包房费100元时，包房便可全部租出。若每间包房收费提高20元，则减少10间包房租出；若每间包房收费再提高20元，-九年级数学

[db:作者] 2019-12-17 00:00:00 互联网

题文

凯里市某大型酒店有包房100间，在每天晚餐营业时间，每间包房收包房费100元时，包房便可全部租出。若每间包房收费提高20元，则减少10间包房租出；若每间包房收费再提高20元，则再减少10间包房租出。以每次提高20元的这种方法变化下去。
（1）设每间包房收费提高x（元），则每间包房的收入为y₁（元），但会减少y₂间包房租出，请分别写出y₁、y₂与x之间的函数关系式；
（2）为了投资少而利润大，每间包房提高x（元）后，设酒店老板每天晚餐包房总收入为y（元），请写出y与x之间的函数关系式，求出每间包房每天晚餐应提高多少元可获得最大包房费收入，并说明理由。
题型：解答题难度：中档

答案

解：（1）；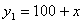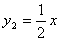
（2），
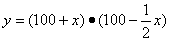即y，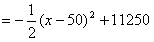
因为提价前包房费总收入为100×100=10000。
当x=50时，可获最大包房收入11250元，又11250>10000。又因为每次提价为20元，所以每间包房晚餐应提高40元或60元。

据专家权威分析，试题“凯里市某大型酒店有包房100间，在每天晚餐营业时间，每间包房收包..”主要考查你对求二次函数的解析式及二次函数的应用，求一次函数的解析式及一次函数的应用等考点的理解。关于这些考点的“档案”如下：

求二次函数的解析式及二次函数的应用求一次函数的解析式及一次函数的应用

考点名称：求二次函数的解析式及二次函数的应用

求二次函数的解析式：
最常用的方法是待定系数法，根据题目的特点，选择恰当的形式，一般，有如下几种情况：
（1）已知抛物线上三点的坐标，一般选用一般式；
（2）已知抛物线顶点或对称轴或最大（小）值，一般选用顶点式；
（3）已知抛物线与x轴的两个交点的横坐标，一般选用两点式；
（4）已知抛物线上纵坐标相同的两点，常选用顶点式。

二次函数的应用：
（1）应用二次函数才解决实际问题的一般思路：
理解题意；
建立数学模型；
解决题目提出的问题。
（2）应用二次函数求实际问题中的最值：
即解二次函数最值应用题，设法把关于最值的实际问题转化为二次函数的最值问题，然后按求二次函数最值的方法求解。
求最值时，要注意求得答案要符合实际问题。
二次函数的三种表达形式：
①一般式：
y=ax2+bx+c(a≠0,a、b、c为常数)，顶点坐标为 [,]
把三个点代入函数解析式得出一个三元一次方程组，就能解出a、b、c的值。

②顶点式：
y=a(x-h)2+k(a≠0,a、h、k为常数),顶点坐标为对称轴为直线x=h，顶点的位置特征和图像的开口方向与函数y=ax²的图像相同，当x=h时，y最值=k。
有时题目会指出让你用配方法把一般式化成顶点式。
例：已知二次函数y的顶点(1,2)和另一任意点(3,10)，求y的解析式。
解：设y=a(x-1)2+2，把(3,10)代入上式，解得y=2(x-1)2+2。
注意：与点在平面直角坐标系中的平移不同，二次函数平移后的顶点式中，h>0时，h越大，图像的对称轴离y轴越远，且在x轴正方向上，不能因h前是负号就简单地认为是向左平移。
具体可分为下面几种情况：
当h>0时，y=a(x-h)2的图象可由抛物线y=ax2向右平行移动h个单位得到；
当h<0时，y=a(x-h)2的图象可由抛物线y=ax2向左平行移动|h|个单位得到；
当h>0,k>0时，将抛物线y=ax2向右平行移动h个单位，再向上移动k个单位，就可以得到y=a(x-h)2+k的图象；
当h>0,k<0时，将抛物线y=ax2向右平行移动h个单位，再向下移动|k|个单位可得到y=a(x-h)2+k的图象；
当h<0,k>0时，将抛物线y=ax2向左平行移动|h|个单位，再向上移动k个单位可得到y=a(x-h)2+k的图象；
当h<0,k<0时，将抛物线y=ax2向左平行移动|h|个单位，再向下移动|k|个单位可得到y=a(x-h)2+k的图象。

③交点式：
y=a(x-x₁)(x-x₂) (a≠0) [仅限于与x轴即y=0有交点时的抛物线，即b²-4ac≥0] .
已知抛物线与x轴即y=0有交点A（x₁，0）和 B（x₂，0）,我们可设y=a(x-x₁)(x-x₂),然后把第三点代入x、y中便可求出a。

由一般式变为交点式的步骤：
二次函数
∵x₁+x₂=-b/a， x₁?x₂=c/a(由韦达定理得),
∴y=ax2+bx+c
=a(x2+b/ax+c/a)
=a[x2-(x₁+x₂)x+x₁?x₂]
=a(x-x₁)(x-x₂).
重要概念：
a，b，c为常数，a≠0，且a决定函数的开口方向。a>0时，开口方向向上；
a<0时，开口方向向下。a的绝对值可以决定开口大小。
a的绝对值越大开口就越小，a的绝对值越小开口就越大。
能灵活运用这三种方式求二次函数的解析式；
能熟练地运用二次函数在几何领域中的应用；
能熟练地运用二次函数解决实际问题。
二次函数的其他表达形式：
①牛顿插值公式:
f(x)=f[x₀]+f[x₀,x₁](x-x₀)+f[x₀,x₁,x₂](x-x₀)(x-x₁)+...f[x₀,...x_n](x-x₀)...(x-_xn-1)+Rn(x)由此可引导出交点式的系数a=y/(x·x)(y为截距)　
二次函数表达式的右边通常为二次三项式。

双根式
y=a(x-x₁)*(x-x2)
若ax2+bx+c=0有两个实根x₁,x₂，则y=a(x-x₁)(x-x₂)此抛物线的对称轴为直线x=(x₁+x₂)/2。

③三点式
已知二次函数上三个点，（x₁,f(x₁)）（x₂,f(x₂)）（x₃,f(x₃)）
则f(x)=f(x₃)(x-x₁)(x-x₂)/(x₃-x₁)(x₃-x₂)+f(x₂)(x-x₁)*(x-x₃)/(x₂-x₁)(x₂-x₃)+f(x₁)(x-x₂)(x-x₃)/(x₁-x₂)(x₁-x₃)
与X轴交点的情况
当△=b2-4ac>0时，函数图像与x轴有两个交点。(x₁,0), (x₂,0);
当△=b2-4ac=0时，函数图像与x轴只有一个交点。(-b/2a，0)。
Δ=b2-4ac<0时，抛物线与x轴没有交点。
X的取值是虚数（x=-b±√b2－4ac的值的相反数，乘上虚数i，整个式子除以2a）
二次函数解释式的求法：
就一般式y=ax2＋bx＋c（其中a，b，c为常数，且a≠0）而言，其中含有三个待定的系数a ，b ，c．求二次函数的一般式时，必须要有三个独立的定量条件，来建立关于a ，b ，c 的方程，联立求解，再把求出的a ，b ，c 的值反代回原函数解析式，即可得到所求的二次函数解析式。

1.巧取交点式法：
知识归纳：二次函数交点式：y＝a(x－x₁)(x－x₂) （a≠0）x₁，x₂分别是抛物线与x轴两个交点的横坐标。
已知抛物线与x轴两个交点的横坐标求二次函数解析式时，用交点式比较简便。
①典型例题一：告诉抛物线与x轴的两个交点的横坐标，和第三个点，可求出函数的交点式。
例：已知抛物线与x轴交点的横坐标为-2和1 ，且通过点（2，8），求二次函数的解析式。
点拨：
解设函数的解析式为y＝a(x+2)(x-1)，
∵过点（2，8），
∴8＝a(2+2)(2-1)。
解得a=2，
∴抛物线的解析式为：
y＝2(x+2)(x-1)，
即y＝2x2+2x-4。

②典型例题二：告诉抛物线与x轴的两个交点之间的距离和对称轴，可利用抛物线的对称性求解。
例：已知二次函数的顶点坐标为（3，-2），并且图象与x轴两交点间的距离为4，求二次函数的解析式。
点拨：
在已知抛物线与x轴两交点的距离和顶点坐标的情况下，问题比较容易解决．由顶点坐标为（3，-2）的条件，易知其对称轴为x＝3，再利用抛物线的对称性，可知图象与x轴两交点的坐标分别为（1，0）和（5，0）。此时，可使用二次函数的交点式，得出函数解析式。

2.巧用顶点式：
顶点式y=a(x－h)²+k（a≠0），其中（h，k）是抛物线的顶点。当已知抛物线顶点坐标或对称轴，或能够先求出抛物线顶点时，设顶点式解题十分简洁，因为其中只有一个未知数a。在此类问题中，常和对称轴，最大值或最小值结合起来命题。在应用题中，涉及到桥拱、隧道、弹道曲线、投篮等问题时，一般用顶点式方便．
①典型例题一：告诉顶点坐标和另一个点的坐标，直接可以解出函数顶点式。
例：已知抛物线的顶点坐标为（-1，-2），且通过点（1，10），求此二次函数的解析式。
点拨：
解∵顶点坐标为（-1，-2），
故设二次函数解析式为y=a(x+1)²-2 （a≠0）。
把点（1，10）代入上式，得10=a·(1+1)²-2。
∴a=3。
∴二次函数的解析式为y=3(x+1)²-2，即y=3x²+6x+1。

②典型例题二：
如果a>0，那么当时，y有最小值且y_最小=；
如果a<0，那么，当时，y有最大值，且y_最大=。
告诉最大值或最小值，实际上也是告诉了顶点坐标，同样也可以求出顶点式。
例：已知二次函数当x＝4时有最小值－3，且它的图象与x轴两交点间的距离为6，求这个二次函数的解析式。
点拨：
析解∵二次函数当x＝4时有最小值－3，∴顶点坐标为（4，-3），对称轴为直线x＝4，抛物线开口向上。
由于图象与x轴两交点间的距离为6，根据图象的对称性就可以得到图象与x轴两交点的坐标是（1，0）和（7，0）。
∴抛物线的顶点为（4，-3）且过点（1，0）。
故可设函数解析式为y＝a(x－4)²－3。
将（1，0）代入得0＝a(1－4)²－3, 解得a＝13．
∴y＝13(x－4)²-3，即y＝13x²－83x＋73。
③典型例题三：告诉对称轴，相当于告诉了顶点的横坐标，综合其他条件，也可解出。
例如：
（1）已知二次函数的图象经过点A（3，-2）和B（1，0），且对称轴是直线x＝3．求这个二次函数的解析式.
（2）已知关于x的二次函数图象的对称轴是直线x=1，图象交y轴于点（0，2），且过点（-1，0），求这个二次函数的解析式.
（3）已知抛物线的对称轴为直线x=2，且通过点（1，4）和点（5，0），求此抛物线的解析式.
（4）二次函数的图象的对称轴x=-4，且过原点，它的顶点到x轴的距离为4，求此函数的解析式．

④典型例题四：利用函数的顶点式，解图像的平移等问题非常方便。
例：把抛物线y=ax2+bx+c的图像向右平移3 个单位, 再向下平移2 个单位, 所得图像的解析式是y=x2-3x+5, 则函数的解析式为_______。
点拨：
解先将y=x2-3x+5化为y=(x-32)2+5-94, 即y=(x-32)2+114。
∵它是由抛物线的图像向右平移3 个单位, 再向下平移2 个单位得到的，
∴原抛物线的解析式是y=(x-32+3)2+114+2=(x+32)2+194=x2+3x+7。

考点名称：求一次函数的解析式及一次函数的应用

待定系数法求一次函数的解析式：
先设出函数解析式，再根据条件确定解析式中的未知系数，从而得到函数的解析式的方法。

一次函数的应用：
应用一次函数解应用题，一般是先写出函数解析式，在依照题意，设法求解。
（1）有图像的，注意坐标轴表示的实际意义及单位；
（2）注意自变量的取值范围。
用待定系数法求一次函数解析式的四个步骤：
第一步（设）：设出函数的一般形式。（称一次函数通式）
第二步（代）：代入解析式得出方程或方程组。
第三步（求）：通过列方程或方程组求出待定系数k，b的值。
第四步（写）：写出该函数的解析式。

一次函数的应用涉及问题：
一、分段函数问题
分段函数是在不同区间有不同对应方式的函数，要特别注意自变量取值范围的划分，既要科学合理，又要符
合实际。

二、函数的多变量问题
解决含有多变量问题时，可以分析这些变量的关系，选取其中一个变量作为自变量，然后根据问题的条件寻
求可以反映实际问题的函数

三、概括整合
（1）简单的一次函数问题：①建立函数模型的方法；②分段函数思想的应用。
（2）理清题意是采用分段函数解决问题的关键。

生活中的应用：
1.当时间t一定，距离s是速度v的一次函数。s=vt。
2.如果水池抽水速度f一定，水池里水量g是抽水时间t的一次函数。设水池中原有水量S。g=S-ft。
3.当弹簧原长度b（未挂重物时的长度）一定时，弹簧挂重物后的长度y是重物重量x的一次函数，即y=kx+b（k为任意正数）
一次函数应用常用公式：
1.求函数图像的k值：（y₁-y₂)/(x₁-x₂)
2.求与x轴平行线段的中点：(x₁+x₂)/2
3.求与y轴平行线段的中点：(y₁+y₂)/2
4.求任意线段的长：√[(x₁-x₂)²+(y₁-y₂)² ]
5.求两个一次函数式图像交点坐标：解两函数式
两个一次函数 y₁=k₁x+b₁; y₂=k₂x+b₂ 令y₁=y₂得k₁x+b₁=k₂x+b₂ 将解得的x=x0值代回y₁=k₁x+b₁ ; y₂=k₂x+b₂ 两式任一式得到y=y₀ 则(x₀,y₀)即为 y₁=k₁x+b₁与 y₂=k₂x+b₂ 交点坐标
6.求任意2点所连线段的中点坐标：[（x₁+x₂）/2，（y₁+y₂）/2]
7.求任意2点的连线的一次函数解析式：（x-x₁）/(x₁-x₂)=(y-y₁)/(y₁-y₂) (若分母为0，则分子为0)
（x,y）为 + ，+（正，正）时该点在第一象限
（x,y）为 - ，+（负，正）时该点在第二象限
（x,y）为 - ，-（负，负）时该点在第三象限
（x,y）为 + ，-（正，负）时该点在第四象限
8.若两条直线y₁=k₁x+b₁//y₂=k₂x+b₂，则k₁=k₂，b₁≠b₂
9.如两条直线y₁=k₁x+b₁⊥y₂=k₂x+b₂，则k₁×k₂=-1
10.
y=k（x-n）+b就是直线向右平移n个单位
y=k（x+n）+b就是直线向左平移n个单位
y=kx+b+n就是向上平移n个单位
y=kx+b-n就是向下平移n个单位
口决：左加右减相对于x，上加下减相对于b。
11.直线y=kx+b与x轴的交点：(-b/k，0) 与y轴的交点：(0，b)

http://www.00-edu.com/ks/shuxue/2/120/2019-12-18/1874555.html十二生肖
十二星座